Hobbyelektriker
· Värmland, Molkom
· 26 144 inlägg
Här är en sammanställning av 60127 (glasrörssäkringar)
Jag tror keramiska finsäkringar också byggs under samma standard. Dock väldigt osäker på detta för det är okända marker för mig (finsäkringar)
Intressant tabell. Vad räknar man som hög, låg, bättre brytförmåga?
Intressant tabell. Vad räknar man som hög, låg, bättre brytförmåga?
Hobbyelektriker
· Värmland, Molkom
· 26 144 inlägg
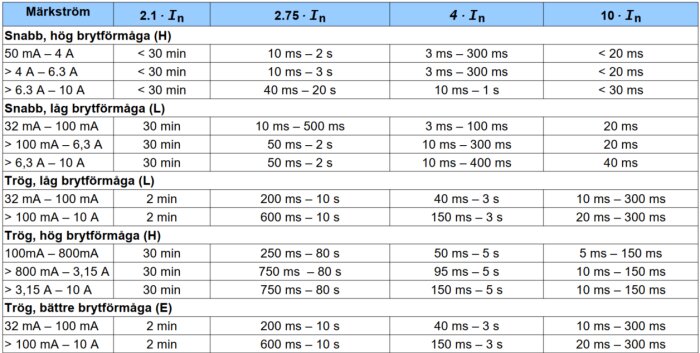
H – Hög, 1.5 kA. Brukar mycket riktigt vara utförda som keramikhus med sand kring säkringstråden.
E – Enhanced, 150 A.
L – Låg, 10 x märkströmmen men lägst 35 A. Brukar vara utförda som glasrör med luft kring säkringstråden.
E – Enhanced, 150 A.
L – Låg, 10 x märkströmmen men lägst 35 A. Brukar vara utförda som glasrör med luft kring säkringstråden.
Keramiska brukar vara sandfyllda H-säkringar (hög brytförmåga).
Man kan ofta se på märkningen om det är IEC 60127, de är märkta typ F100mAH. D.v.s snabbhet, ström och brytkapacitet.
Står det på nåt annat sätt (t.ex. 100 mA T) så är det inte IEC 60127.
Man kan ofta se på märkningen om det är IEC 60127, de är märkta typ F100mAH. D.v.s snabbhet, ström och brytkapacitet.
Står det på nåt annat sätt (t.ex. 100 mA T) så är det inte IEC 60127.
Det är ju samma tänk med finsäkringar och dimensionering dock behöver man nog beakta genomsläppt energi och att brytförmågan inte överskrids mer noggrant jämfört med en vanlig elinstallation i ett hus.
Jag håller fortfarande på och tragglar med detta, dvs det som ledde mig till att jag var tvungen att få koll på bl.a. glasrörssäkringar.
Det gäller dimensionering av klenspänningsinstallationer, i mitt fall fokus på 24VAC, men det kommer förstås vara lika giltigt för andra spänningar.
Min plan är dessutom att göra en kunskapsåterföring till forumet sen.
Men nu har jag lite mer frågor, som berör ingångsvärden för sådan här kabel och säkringsdimensionering, och jag funderar just nu på transformatorer.
Så, in i ämnet, och sen min fråga, jag hoppas det finns några på forumet som kan svara.
Ett allmänt schema över en trafo
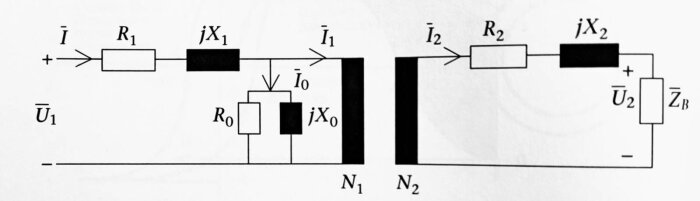
Bild 1
U1 matningsspänning, ... U2 sekundärspänning och ZB last.
N1 och N2 antal lindningvarv (N1/N2 = lindningsomsättning, varvomsättning)
R1 och R2 är resistanser på primär resp sekundärsida, jX1 och jX2 är reaktanser som i princip beror på läckreaktanser.
R0 och jX0 är det som motsvarar transformatorn tomgångsförluster, virvelströmmar och läckreaktanser som uppstår pga transformatorns grundmagnetisering.
Dessa är jag just nu inte intresserad av.
Så därför är detta en bättre bild, denna bild visar även en sk kortslutningsprov, sekundärlindningen kortsluten, samt beteckningarna U1K, I1K och I2K berättar att detta visar ett kortslutningsprov.
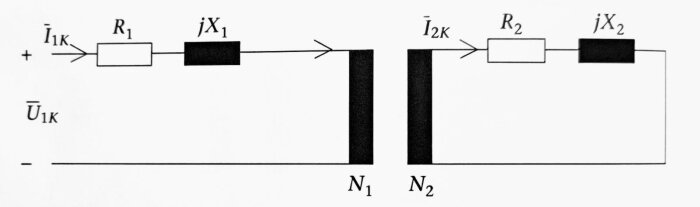
Bild 2
För att bestämma en transformators egenskaper så kan man utföra ett tomgångsprov och ett kortslutningsprov, vi det senare så kortsluter man sekundärutgången på transformatorn (eller egentligen den sida med lägst märkspänning) och sen matar man in den spänning på primärlindningen som gör att det går märkström, så i praktiken matar man transformatorn med några procent av märkspänningen.
Vid detta prov kan man överföra alla resistanser och reaktanser till antingen primär eller sekundärsidan genom att använda lindningsomsättningstalet.
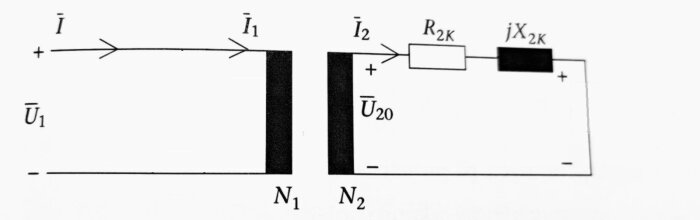
Bild 3
Här en bild när resistans och reaktans är överfört till sekundärsidan.
Efter kortslutningsprovet kan man räkna fram en viktig parameter, uk (kallas ibland uz) och kallas ofta transformatorns procentuella kortslutningsspänning eller bara kortslutningsspänning. Anges ofta, men inte alltid i procent.
Denna faktor anger hur många procent spänningen faller på sekundärlindningen vid full märklast jämfört med vid tomgång. (går också att räkna om till primärsidan om man vill osv).
Det gäller dimensionering av klenspänningsinstallationer, i mitt fall fokus på 24VAC, men det kommer förstås vara lika giltigt för andra spänningar.
Min plan är dessutom att göra en kunskapsåterföring till forumet sen.
Men nu har jag lite mer frågor, som berör ingångsvärden för sådan här kabel och säkringsdimensionering, och jag funderar just nu på transformatorer.
Så, in i ämnet, och sen min fråga, jag hoppas det finns några på forumet som kan svara.
Ett allmänt schema över en trafo
Bild 1
U1 matningsspänning, ... U2 sekundärspänning och ZB last.
N1 och N2 antal lindningvarv (N1/N2 = lindningsomsättning, varvomsättning)
R1 och R2 är resistanser på primär resp sekundärsida, jX1 och jX2 är reaktanser som i princip beror på läckreaktanser.
R0 och jX0 är det som motsvarar transformatorn tomgångsförluster, virvelströmmar och läckreaktanser som uppstår pga transformatorns grundmagnetisering.
Dessa är jag just nu inte intresserad av.
Så därför är detta en bättre bild, denna bild visar även en sk kortslutningsprov, sekundärlindningen kortsluten, samt beteckningarna U1K, I1K och I2K berättar att detta visar ett kortslutningsprov.
Bild 2
För att bestämma en transformators egenskaper så kan man utföra ett tomgångsprov och ett kortslutningsprov, vi det senare så kortsluter man sekundärutgången på transformatorn (eller egentligen den sida med lägst märkspänning) och sen matar man in den spänning på primärlindningen som gör att det går märkström, så i praktiken matar man transformatorn med några procent av märkspänningen.
Vid detta prov kan man överföra alla resistanser och reaktanser till antingen primär eller sekundärsidan genom att använda lindningsomsättningstalet.
Bild 3
Här en bild när resistans och reaktans är överfört till sekundärsidan.
Efter kortslutningsprovet kan man räkna fram en viktig parameter, uk (kallas ibland uz) och kallas ofta transformatorns procentuella kortslutningsspänning eller bara kortslutningsspänning. Anges ofta, men inte alltid i procent.
Denna faktor anger hur många procent spänningen faller på sekundärlindningen vid full märklast jämfört med vid tomgång. (går också att räkna om till primärsidan om man vill osv).
Då uk alltid finns som en siffra i datablad när man kikar på stora transformatorer för distributionsnätet så är det inte alls lika säkert att hitta något för mindre transformatorer för t.ex. 24VAC.
Men t.ex. Schneider har denna uppgift för ett stort antal av sina, t.ex.
https://docs.rs-online.com/6bdc/0900766b810a39fa.pdf
Heter här Short-circuit voltage då detta är ett datablad på engelska, och värdet uppges till 0,0786
Dvs, Schneider väljer att inte följa det normala att ange det i procent, så det är alltså 7,86% här.
Lite data på några få Schneider-trafos:
Sen har jag en kolumn med Ri, jag återkommer till den.
Vad gör man ifall man inte har denna data i databladet då?
T.ex. Tufvasson har diagram över spänningsfall, det måste väl kunna användas.
Kan se ut såhär:
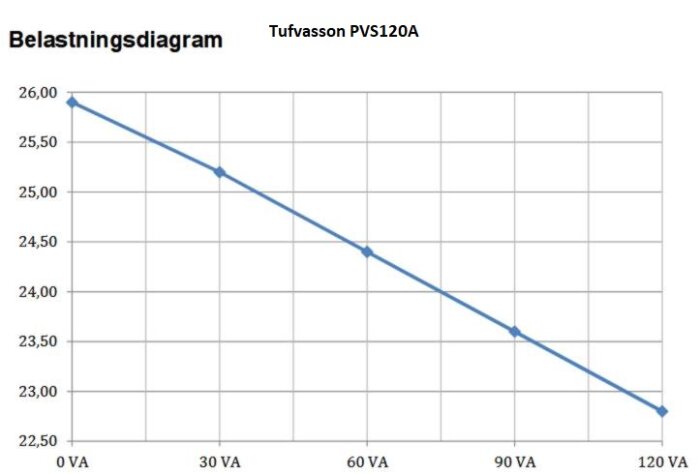
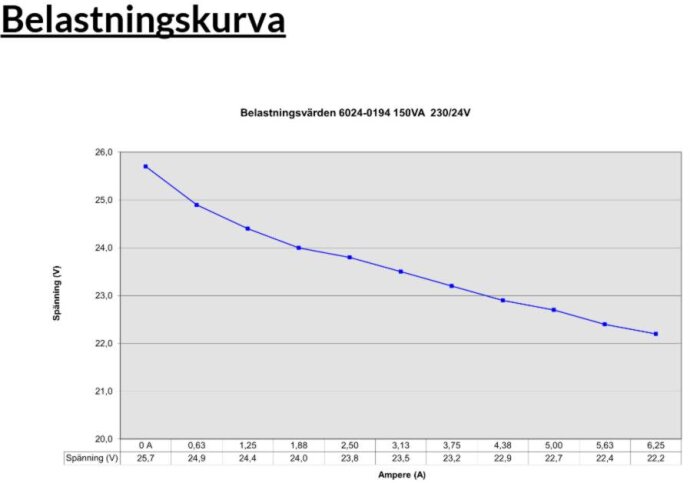
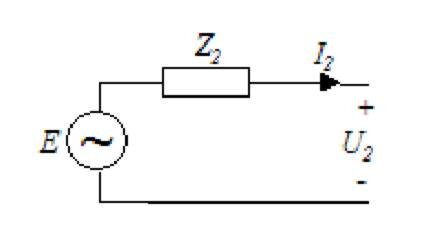
Och då tänker jag att genom att mäta spänning vid noll last och vid full last, och dela deltaU med deltaI så får man fram den inre resistansen, typ som denna bild:
Men t.ex. Schneider har denna uppgift för ett stort antal av sina, t.ex.
https://docs.rs-online.com/6bdc/0900766b810a39fa.pdf
Heter här Short-circuit voltage då detta är ett datablad på engelska, och värdet uppges till 0,0786
Dvs, Schneider väljer att inte följa det normala att ange det i procent, så det är alltså 7,86% här.
Lite data på några få Schneider-trafos:
| Transformator | P [VA] | U [V] | I [A] | zk | Ri [Ω] |
| Schneider ABL6TS10B | 100 | 24 | 4,2 | 0,0786 | 0,45 |
| Schneider ABT7ESM010B | 100 | 24 | 4,2 | 0,113 | 0,65 |
| Schneider ABT7ESM025B | 250 | 24 | 10,4 | 0,083 | 0,19 |
| Schneider ABT7ESM032B | 320 | 24 | 13,3 | 0,062 | 0,11 |
Sen har jag en kolumn med Ri, jag återkommer till den.
Vad gör man ifall man inte har denna data i databladet då?
T.ex. Tufvasson har diagram över spänningsfall, det måste väl kunna användas.
Kan se ut såhär:
Och då tänker jag att genom att mäta spänning vid noll last och vid full last, och dela deltaU med deltaI så får man fram den inre resistansen, typ som denna bild:
Och nu börjar jag närma mig min fråga.
Är denna sista bild en helt giltig approximation över en transformators förmåga att skicka ut ström, och vilket spänningsfall som sker.
Om jag struntar i mindre detaljer, kan jag tänka att det finns en ideal spänningskälla + inre impedans (resistans) som gäller hyggligt alltifrån tomgång till stum kortslutning?
För vad det gäller Tufvasontrafo PVS120A så kan jag t.ex. ta ut 25,9V och 22,8V vid 0VA (0A) resp 120VA (5A) och räkna ut Z2 = (25,9 - 22,8)/ (5A - 0A)= 0,62 ohm.
Dvs att den inre impedansen skulle vara 0,62 ohm.
Och belastar jag denna trafo med totalt 1 ohm i ledningarna fram till en kortslutning, så kommer denna trafo att mata ut 24/(1 + 0,62) = 14,8 A.
Och skulle jag kortsluta direkt på utgången av transformatorn skulle strömmen bli 24/0,62 = 38,7 A
Är denna sista bild en helt giltig approximation över en transformators förmåga att skicka ut ström, och vilket spänningsfall som sker.
Om jag struntar i mindre detaljer, kan jag tänka att det finns en ideal spänningskälla + inre impedans (resistans) som gäller hyggligt alltifrån tomgång till stum kortslutning?
För vad det gäller Tufvasontrafo PVS120A så kan jag t.ex. ta ut 25,9V och 22,8V vid 0VA (0A) resp 120VA (5A) och räkna ut Z2 = (25,9 - 22,8)/ (5A - 0A)= 0,62 ohm.
Dvs att den inre impedansen skulle vara 0,62 ohm.
Och belastar jag denna trafo med totalt 1 ohm i ledningarna fram till en kortslutning, så kommer denna trafo att mata ut 24/(1 + 0,62) = 14,8 A.
Och skulle jag kortsluta direkt på utgången av transformatorn skulle strömmen bli 24/0,62 = 38,7 A
Du kan i dina fall helt utgå från Ri antingen från uppgifter likt Schneiders eller tagna via beräkning från grafer eller egna prov i två punkter. Kombinationen Xk och Rk som ger ett Zk kommer här inte bli annat än att R dominerar så bara att ta nominella spänningen och dividera med Ri så får man strömmen direkt vid trafon eller lägga med bidraget från yttre kretsen vid dimensionering av helheten.
Om man vill använda uppgiften i tabellen från Schneider är det bara att ta märkströmmen för trafon och dividera med zk så har man kortslutningsströmmen direkt på uttagen. resultatet blir i praktiken samma inget man behöver skilja på för att bedöma avsäkringen av en sån krets som här tex typisk stryr-regler matning.
Om man vill använda uppgiften i tabellen från Schneider är det bara att ta märkströmmen för trafon och dividera med zk så har man kortslutningsströmmen direkt på uttagen. resultatet blir i praktiken samma inget man behöver skilja på för att bedöma avsäkringen av en sån krets som här tex typisk stryr-regler matning.
Det går att räkna ut vad denna inre impedans Z2 blir utifrån att man har kortslutningsspänningen.
Med denna formel
UK = ( I2M * Z2K )/ ( U2M ) * 100
( I2M och U2M är märkström och märkspänning)
Så Z2K = ( UK * U2M * 100) / I2M
Vilket ger för t.ex. schneidertrafon i PDF-länken Z2K = ( UK * U2M )/ I2M = 0,0786 * 24 / 4,2 = 0,45 ohm.
(Jag tog bort 100, för att Schneider anger inte i procent).
Och på detta sätt har jag skapat kolumnen för Ri
Med denna formel
UK = ( I2M * Z2K )/ ( U2M ) * 100
( I2M och U2M är märkström och märkspänning)
Så Z2K = ( UK * U2M * 100) / I2M
Vilket ger för t.ex. schneidertrafon i PDF-länken Z2K = ( UK * U2M )/ I2M = 0,0786 * 24 / 4,2 = 0,45 ohm.
(Jag tog bort 100, för att Schneider anger inte i procent).
Och på detta sätt har jag skapat kolumnen för Ri
Ja, jag trodde på vad jag kommit fram till.
Men sen när jag började räkna lite på strömmar, och räknade på Schneider-trafon på 320 VA, så blev ju Z2 = 0,11 ohm, och sen om modellen med ideal spänningskälla och endast Z2 som bestämmer strömmen så skulle denna trafo då mata ut 220 A vid stum kortslutning direkt på utgången.
Och nu började jag plötsligt tveka, har jag verkligen rätt.
Kan den där relativt lilla klumpen, verkligen mata ut över 200 A.
Men du verkar hålla med mig i alla fall.
Det bli samma om jag räknar på I2M / zk (215 A). som du föreslog.
(Och ja, det är ju bara omkastande av faktorer eller ta bort onödiga led i beräkningarna, man behöver inte blanda in märkspänningen t.ex.)
Men sen när jag började räkna lite på strömmar, och räknade på Schneider-trafon på 320 VA, så blev ju Z2 = 0,11 ohm, och sen om modellen med ideal spänningskälla och endast Z2 som bestämmer strömmen så skulle denna trafo då mata ut 220 A vid stum kortslutning direkt på utgången.
Och nu började jag plötsligt tveka, har jag verkligen rätt.
Kan den där relativt lilla klumpen, verkligen mata ut över 200 A.
Men du verkar hålla med mig i alla fall.
Det bli samma om jag räknar på I2M / zk (215 A). som du föreslog.
(Och ja, det är ju bara omkastande av faktorer eller ta bort onödiga led i beräkningarna, man behöver inte blanda in märkspänningen t.ex.)
Jag har också hittat denna formel (som verkar användas för att beräkna kortslutningseffekter i nätavsnitt).
SK = SM/ zk
Skenbar kortslutningseffekt = märkeffekt (skenbar) delat med zk
Så med den där 320VA-trafon blir det 320/ 0.062 = 5162 VA, 5,2 kVA !
Räknar jag på kortslutningsströmmen 220A och märkspänning, 220 * 24 = 5,3 kVA
Ungefär samma, så det verkar ju också stämma.
Men det hela stämmer till lite eftertanke, ska dessa strömmar och effekter uppnås vid kortslutning så måste överströmsskydd vara rejält tilltagna på matningssidan, trafon kommer ju att dra 22-23A på primärsidan.
Och likaså kommer allt detta bli värme i transformatorn, den lär inte tåla detta speciellt många sekunder.
Så i praktiken kanske de teoretisk högsta kortslutningsströmmarna blir lite begränsade trots allt.
SK = SM/ zk
Skenbar kortslutningseffekt = märkeffekt (skenbar) delat med zk
Så med den där 320VA-trafon blir det 320/ 0.062 = 5162 VA, 5,2 kVA !
Räknar jag på kortslutningsströmmen 220A och märkspänning, 220 * 24 = 5,3 kVA
Ungefär samma, så det verkar ju också stämma.
Men det hela stämmer till lite eftertanke, ska dessa strömmar och effekter uppnås vid kortslutning så måste överströmsskydd vara rejält tilltagna på matningssidan, trafon kommer ju att dra 22-23A på primärsidan.
Och likaså kommer allt detta bli värme i transformatorn, den lär inte tåla detta speciellt många sekunder.
Så i praktiken kanske de teoretisk högsta kortslutningsströmmarna blir lite begränsade trots allt.
HejGK100 skrev:
Jag håller inte med om att det är resistansen R som dominerar i en transformators indre impedans Z
Utan det är snarare reaktansen X som dominerar
Dessutom ser jag inte, i det som ni två räknar, hur ni två hanterar att X och R är 90 grader fasförskjutna gentemot varandra och att impedansen (Z) därmed är hypotenusan av de båda vektorerna X och R
Redigerat:
Begränsas inte strömmen även av att kärnan går i mättnad?
Det har var länge sen...🤔
Det har var länge sen...🤔
Tja, genom att räkna med Z, inte R eller XL.M Martin Lundmark skrev: