Förimpedans

[Bo.Siltberg]

I mätarskåpet kanske 350 mΩ är för mycket, men inte i centralen.
Jag har 670 mΩ i mätarskåpet och en dryg Ω i första centralen...
Transformatorkiosken står 500 meter bort. Vad brukar det vara för area på hängspiralkabel?

 

[spinout]

350mΩ låter normalt tycker jag för tätbebyggelse. Men även på landet är det bra också, i alla fall här i krokarna, upplever jag det som i alla fall.

 

[lars_stefan_axelsson]

Tack alla som svarat; Gott, då är vi i alla fall inte helt ute och cyklar. Även om det tydligen ligger i högsta laget för "mitt inne i stan". Jag pratade med Göteborg Energi idag och efter ett gott skratt åt min mätmetod så lovade ingenjören att skicka en fullständig beräkning (jag har tydligen ungefär knappt 100m till min transformatorstation och en 10mm Alu-kabel till skåpet som står på vändplan kanske 10m från husknuten. Mycket_nu; ja, jag har bara någon decimeter från mätaren till centralen, MEN, eftersom huset från början hade luftledning så har jag ett separat skåp inne i hörnet på källaren till servissäkringarna och sedan kanske sju meter eller så till mätarsäkringarna, så jag antar att jag måste kompensera för det (men det är ju bara att kolla hur grov kabeln är och göra en skattning).

Jag återkommer när jag fått resultatet. Han lovade ett "skolboksexempel" på hur GbgEnergi presenterar förimpedans.

P.S. När vi tog fram mitt servisnummer så visade det sig att GbgEnergi har ett trevligt sätt att namnge sina kablar. De döpte helt enkelt sin första kabel till "1", den andra till "2" och så har det fortsatt. Min egen servis heter något på 900000. Och nej, kabel 1 är inte längre i drift.

 

[lars_stefan_axelsson]

Hmm, jag kan inte se annat än att det räcker med en (extra) belastning för att sen mäta på en (extra) spänningssänkning.
Dvs jag tror inte att en grundlast av något slag förändrar värdet. Det enda som är viktigt är att ingen belastning slog till eller ifrån momentant mellan de två späningsmätningarna.

OK, jag får erkänna mig besegrad. Jag har vridit och vänt på diagrammet nedan några gånger men får ändå en obekant för mycket när jag ställer ekvationerna.

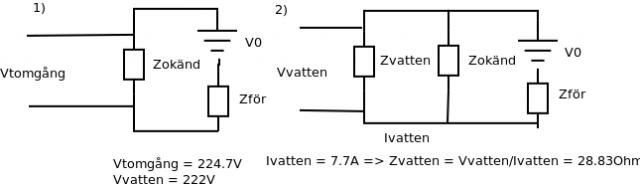
Någon får hemskt gärna leda vid mig handen och tala om hur man kan lösa ut Zför ur fallen nedan utan att anta att i0=0, dvs att Zokänd är oändlig (eller i alla fall stor i för hållande till Zvatten(kokare)). Dvs man får en bra approximation om huset inte förbrukar för mycket när man mäter, men om det gör det så kommer man att underskatta Zför, eftersom i0 > 0 och inte försumbar. Var tänker jag fel?

 

[Avemo]

Jag tror att du kan approximera Zokänd till att vara oändlig därför att den är mycket högre än Zför. Jag tänkte inte på det innan, men skall man vara noga så räknar du ut Zför parallellkopplad med Zokänd. Det finns nog större felkällor på andra platser.

Erik

 

[elmont]

Och jag är rätt säker på att du inte har Alu kabel utan en kopparkabel på 10 mm2, 10 mm2 aluminiumkabel är nog en lite främmande fågel.

 

[Bo.Siltberg]

Felet blir litet. Det ser du enklast genom att räkna på exempel med antagna värden för Zför och Zokänd, t.ex 1 och 40 Ω, och 230 V spänning utan Zokänd. Sätt sedan in din vattenvärmare på säg 20 Ω och räkna. Att ställa upp en formel får någon som nyss gått skolan göra...

 

[b_hasse]

Någon får hemskt gärna leda vid mig handen och tala om hur man kan lösa ut Zför ur fallen nedan utan att anta att i0=0, dvs att Zokänd är oändlig (eller i alla fall stor i för hållande till Zvatten(kokare)). Dvs man får en bra approximation om huset inte förbrukar för mycket när man mäter, men om det gör det så kommer man att underskatta Zför, eftersom i0 > 0 och inte försumbar. Var tänker jag fel?

Det räcker att Zokänd är "tillräckligt" mycket större än Zför. Om man ser nätet + Zokänd som en tvåpol så ser man att din mätmetod egentligen ger värdet på Zför parallellkopplat med Zokänd.

Ditt mätvärde Zmätt = (224.7V - 222V) / 7.7A = 0.35 Ohm

1/Zmätt = 1/Zför + 1/Zokänd

1/Zför = 1/Zmätt - 1/Zokänd

Zför = 1 / (1/Zmätt - 1/Zokänd) = (Zokänd * Zmätt) / (Zokänd - Zmätt)

Det största felet får du om du lastar huvudsäkringen maximalt innan mätningen. Vid 20A är Zokänd ca 11.5 Ohm. Trots det blir Zför inte högre än 0.361 Ohm, vilket är väldigt nära de 0.35 du får om du ignorerar Zokänd. Med mer rimliga värden på Zokänd blir förstås felet mindre.

/Hasse

 

[lars_stefan_axelsson]

Tack. Det köper jag. Bara alla är överens om att vi måste göra en approximation så är jag nöjd. Och att approximationen blir bra när man sätter i0=0 är jag också med på. Jag uppfattade tidigare kommentarer som att den kunde bortses från även i teorin och det fick jag inte till.

 

[mycke_nu]

Alternativet är ju att du kopplar bort all last och mäter generatorspänningen obelastad. Sedan är det lätt att bestämma Zokänd.

Notera även att det inte är säkert att Zokänd är positiv. Switchade nätaggregat har negativ inimpedans.

 

[Avemo]

De flesta här är nog mer intresserade av vad som är praktiskt användbart än vad som är teoretiskt riktigt. Därmed inte sagt att det senare skulle vara ointressant. Det jag sett av transformatorer är att spänningen sjunker olinjärt med ökad ström. Det är sannolikt inte en stor felkälla i praktiken, men i teorin gör det förimpedansen hur noga den än mätts eller räknats ut till en linjär approximation av verkligheten. Den kan inte anges exakt annat än under en specifik belastning och temperatur på transformatorn. Det är bra att veta vilka approximationer man gör, men det största felet gör man om man tror att man har ett absolut exakt resultat.

Erik

 

[lars_stefan_axelsson]

De flesta här är nog mer intresserade av vad som är praktiskt användbart än vad som är teoretiskt riktigt. Därmed inte sagt att det senare skulle vara ointressant.
Erik

Speciellt i det här fallet. GbgEnergi skickar ju inte ut en gubbe till mig och *mäter* Zför. De beräknar den teoretiskt och hoppas att denna beräkning stämmer tillräckligt överens med verkligheten för att vara relevant.

För att övertyga sig om detta så måste man ju vara övertygad om att de approximationer man gör är riktiga. Här fick jag inte ens principen att stämma. Sedan är ju beräkningen som sådan full av approximationer i övrigt. Vi gör ju t ex redan en ganska stor approximation genom att sätta Zför = Rför, dvs struntar i den imaginära delen, men den kan jag köpa "i huvudet". (Sedan har vi mätnogrannhet osv.)

 

[lars_stefan_axelsson]

Alternativet är ju att du kopplar bort all last och mäter generatorspänningen obelastad. Sedan är det lätt att bestämma Zokänd.

Visst. Det är ju att sätta i0=0 inte bara i teorin utan även i praktiken. Men det är ju lite fusk. Då blir mätningen helt plötsligt inte lika enkel och smidig. Sedan kan man ju undvika att köra båda tvättmaskinerna, torktumlaren och elpannan samtidig som man mäter, det är en annan sak.

 

[mycke_nu]

Även den reaktiva delen är ganska liten, här hemma så gott som försumbar.

 

[GK100]

Vattenkokarmetoden är väl ett utmärkt sätt att mäta, helt i klass med vad installationstestarna i allmänhet åstadkommer. Finns bättre utrustning av samma princip där halvperiodpulsen kan varieras upp till ca:1000A, då kan man även hitta dåliga anslutningar mm, men givetvis inget för bostadsinstallationer. Vid den mätningen får man en ganska realistisk bild av nätet som helhet även med trafons och de grövre delarnas egenskaper inräknat. En sån uppmätt tvåpol är faktiskt en bra modell att använda vid vidare nätberäkningar.

Ditt värde LSA är nog också ganska representativt, jag vill minnas att större undersökningar av näten vid spänningsomläggningen till 400/230V på 80-talet gav att >90% av abbonnenterna hade bättre än Z = 0.45 + j0.07Ω.
Irland och Polen låg dåligt till med drygt 1Ω och centraleuropa ungefär som här i Sverige, en utstickare var även England som med lite annorlunda nätuppbyggnad låg kring 0.2Ω.