Hej Bo
Det är visserligen mer än 40 år sen jag läste det men är inte fasströmmen förskjuten med 120 grader mellan faserna,och därför går det väl inte att addera fasströmmen som en summa till nollan. Hade det varit 3 faser inblandade lika belastade hade strömmen i nollan blivit 0A
Jag har för mig att det är roten ur 3 alltså 1,73 som är gångerfaktoren / delningsfaktor på strömmen i nollan ? Räta mig om jag är alldeles fel ute, just att det bara är 2 faser inblandade ställer till det.
Det är visserligen mer än 40 år sen jag läste det men är inte fasströmmen förskjuten med 120 grader mellan faserna,och därför går det väl inte att addera fasströmmen som en summa till nollan. Hade det varit 3 faser inblandade lika belastade hade strömmen i nollan blivit 0A
Jag har för mig att det är roten ur 3 alltså 1,73 som är gångerfaktoren / delningsfaktor på strömmen i nollan ? Räta mig om jag är alldeles fel ute, just att det bara är 2 faser inblandade ställer till det.
Hobbyelektriker
· Värmland, Molkom
· 26 131 inlägg
Jodå mycket riktigt är fasströmmen förskjuten med 120 grader mellan faserna så det går inte att addera några strömmar vid tvåfasig belastning. Strömmen i nollan med två och tre belastade faser ser man istället enklast med hjälp av ett visardiagram.
Först och främst så kan vi plocka bort strömmarna mellan faserna. Dessa kan inte ge upphov till någon ström i neutralledaren.
Det är allmänt känt, som du säger, att tre belastade faser som är jämnt belastade ger strömmen 0 i neutralledaren. Figuren till vänster visar dessa tre strömmar, lika långa pilar eftersom strömmen är densamma. Den andra figuren nedan visar summan av dessa tre pilar efter att de vektoradderats. Tag pilen för L2 och placera den där L1 slutar. Flytta sedan L3 på motsvarande sätt. Pilen för L3 kommer då att gå tillbaka till det ställe L1 utgår ifrån, det vill säga det går ingen ström i neutralledaren.
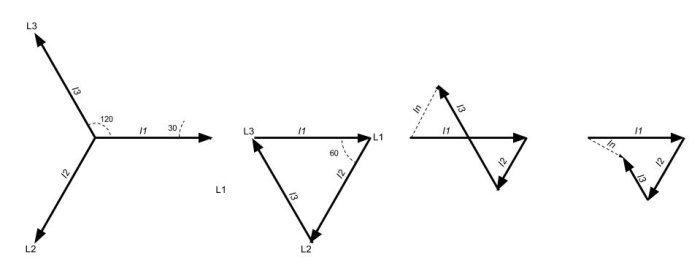
Men om de tre faserna nu inte är jämnt belastade så får vi figurer som de två sista figurerna ovan visar. Strömmen i neutralledaren blir både olika stor och får olika fasvinklar.
De tre vektorerna, när de utgår från origo, bildar en triangel. Vektorn för strömmen i nollan kommer där att peka på mitten av denna triangel.
En tumregel för två belastade faser är att strömmen i neutralledaren blir ungefär lika med den högsta strömmen i endera fasledaren. Detta kan enkelt visas med samma visardiagram. Här ser vi dels att vid lika hög ström i båda faserna så blir strömmen i neutralledaren exakt lika med strömmen i fasledarem, och dels vid olika hög ström så blir strömmen i neutralledaren nästan lika hög som den högsta fasströmmen.
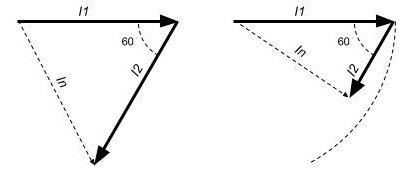
Notera att i samtliga fall, oberoende av antalet faser som leder ström och oberoende av strömmens storlek, så kan inte strömmen i neutralledaren bli högre än i den fasledare som för högst ström. Detta gäller för resistiv last med 120 grader mellan faserna. Fasförskjutning kan ändra på detta, men då i stort alla förbrukare som förskjuter fasen är induktiva så sker fasförskjutningen åt samma håll så resultatet (strömmen i nollan) påverkas inte nämnvärt.
Givetvis går det att räkna på detta. Vi ska alltså summera de två eller tre strömmarna, vilket mycket enkelt görs genom att summera x- och y-koordinaterna för de två eller tre pilarna och slutligen använda Pythagoras sats.
x1 = i1 * cos(0); y1 = i1 * sin(0)
x2 = i2 * cos(-120); y2 = i2 * sin(-120)
In = sqrt( (x1+x2)² + (y1+y2)² )
Om vi sätter in 10 A i L1 och 5 A i L2 så får vi
x1 = 10 * cos(0) = 10; y1 = 10 * sin(0) = 0
x2 = i2 * cos(-120) = - 2.5 ; y2 = i2 * sin(-120) = - 4.33
In = sqrt( (10-2.5)² + (0-4.33)² ) = 8.66 A (stämmer ganska bra med visardiagrammet)
En förenklad formel kan skrivas
IN = I1 /0 + I2 /-120 + I3 /120
Det kan vara värt att inse här att x2 och y2 får negativa värden i beräkningen ovan.
Först och främst så kan vi plocka bort strömmarna mellan faserna. Dessa kan inte ge upphov till någon ström i neutralledaren.
Det är allmänt känt, som du säger, att tre belastade faser som är jämnt belastade ger strömmen 0 i neutralledaren. Figuren till vänster visar dessa tre strömmar, lika långa pilar eftersom strömmen är densamma. Den andra figuren nedan visar summan av dessa tre pilar efter att de vektoradderats. Tag pilen för L2 och placera den där L1 slutar. Flytta sedan L3 på motsvarande sätt. Pilen för L3 kommer då att gå tillbaka till det ställe L1 utgår ifrån, det vill säga det går ingen ström i neutralledaren.
Men om de tre faserna nu inte är jämnt belastade så får vi figurer som de två sista figurerna ovan visar. Strömmen i neutralledaren blir både olika stor och får olika fasvinklar.
De tre vektorerna, när de utgår från origo, bildar en triangel. Vektorn för strömmen i nollan kommer där att peka på mitten av denna triangel.
En tumregel för två belastade faser är att strömmen i neutralledaren blir ungefär lika med den högsta strömmen i endera fasledaren. Detta kan enkelt visas med samma visardiagram. Här ser vi dels att vid lika hög ström i båda faserna så blir strömmen i neutralledaren exakt lika med strömmen i fasledarem, och dels vid olika hög ström så blir strömmen i neutralledaren nästan lika hög som den högsta fasströmmen.
Notera att i samtliga fall, oberoende av antalet faser som leder ström och oberoende av strömmens storlek, så kan inte strömmen i neutralledaren bli högre än i den fasledare som för högst ström. Detta gäller för resistiv last med 120 grader mellan faserna. Fasförskjutning kan ändra på detta, men då i stort alla förbrukare som förskjuter fasen är induktiva så sker fasförskjutningen åt samma håll så resultatet (strömmen i nollan) påverkas inte nämnvärt.
Givetvis går det att räkna på detta. Vi ska alltså summera de två eller tre strömmarna, vilket mycket enkelt görs genom att summera x- och y-koordinaterna för de två eller tre pilarna och slutligen använda Pythagoras sats.
x1 = i1 * cos(0); y1 = i1 * sin(0)
x2 = i2 * cos(-120); y2 = i2 * sin(-120)
In = sqrt( (x1+x2)² + (y1+y2)² )
Om vi sätter in 10 A i L1 och 5 A i L2 så får vi
x1 = 10 * cos(0) = 10; y1 = 10 * sin(0) = 0
x2 = i2 * cos(-120) = - 2.5 ; y2 = i2 * sin(-120) = - 4.33
In = sqrt( (10-2.5)² + (0-4.33)² ) = 8.66 A (stämmer ganska bra med visardiagrammet)
En förenklad formel kan skrivas
IN = I1 /0 + I2 /-120 + I3 /120
Det kan vara värt att inse här att x2 och y2 får negativa värden i beräkningen ovan.
Tack Bo.
Ursäkta att du fick en sömnlös midnatt.
Din pedagogiska förklaring överträffar dom flesta el-lärare i landet.
Den lämnar en förståelse för varför man bör sträva efter flerfasig belastning.
Jag tänker skriva ut den ha den lätt tillgänglig.
Leif i Skåne
Ursäkta att du fick en sömnlös midnatt.
Din pedagogiska förklaring överträffar dom flesta el-lärare i landet.
Den lämnar en förståelse för varför man bör sträva efter flerfasig belastning.
Jag tänker skriva ut den ha den lätt tillgänglig.
Leif i Skåne
Och vad gäller då tredje övertonen, all den strömmen ackumuleras i nollan då alla fasernas tredje överton ligger i fas...
3 år gammalt trådlyft.L Limpan4all skrev:
Om du läser i Bos inlägg så kan fasförskjutning, kombinerat induktivt och kapacitivt orsaka en högre ström i nollan men knappast i en installation av en tvättmaskin och torktumlare som var den ursprungliga frågan i tråden som jag länkade hit för en förklaring av strömmen i nollan.