Medlem
· Västra Götaland
· 231 inlägg
Hej!
Jag vill göra ett trappräcke som stämmer överens med befintligt trapp-"staket". Problemet är att överliggaren är rundad på toppen. Man kan ju hyvla till hyfsad likhet men för nyfikenhetens skull så funderar man på hur man kan mäta/räkna ut radien i fall man skulle vilja fräsa/hyvla till profilen.
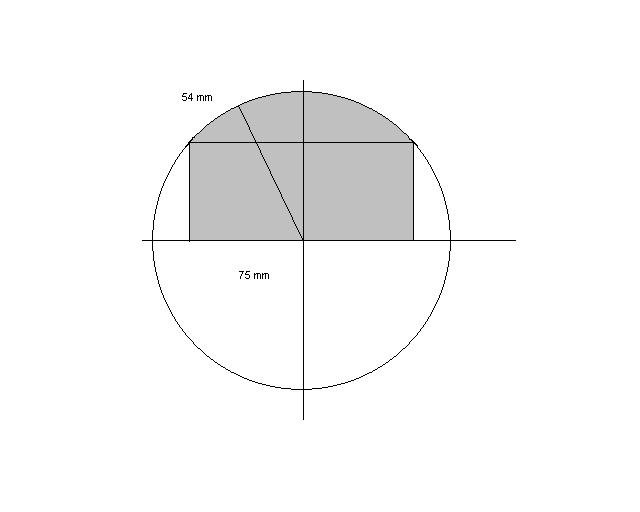
Bifogar en bild som visar genomskärningen.
Jag vill göra ett trappräcke som stämmer överens med befintligt trapp-"staket". Problemet är att överliggaren är rundad på toppen. Man kan ju hyvla till hyfsad likhet men för nyfikenhetens skull så funderar man på hur man kan mäta/räkna ut radien i fall man skulle vilja fräsa/hyvla till profilen.
Bifogar en bild som visar genomskärningen.
Nu är det visserligen tidigt på morgonen och jag hittar inte min formelssamling men...
Mitt ögonmått säger mig att det är mer än 10mm som fattas i skissen för att komma till cirkelns mitt. Såhär räknade jag.
(Ser att min bild inte riktigt hänger ihop men vid punkten B skulle alla linjer mötas på samma ställe.)
Det man skall upptäcka är att triangeln med sidorna c och d har vinkeln B och triangeln med sidorna d och e har vinkeln A. Man skall också inse att vinkeln A = vinkeln B.
Då börjar det roliga.
tan (A) = d/e
tan (B) = c/d
Eftersom A = B är tan (A) = tan (B) och då är
d/e = c/d
d = 75/2
c = 45 - 30 = 15
e = radien - c
75/2e = 15*2 / 75
e = 93,75
radien = 93,75 + 15 = 108,74
Vilket råkar vara dubbelt så mycket som 54,4.
En av våra uträkningar är då fel, jag tror naturligtvis på min.
Mitt ögonmått säger mig att det är mer än 10mm som fattas i skissen för att komma till cirkelns mitt. Såhär räknade jag.
(Ser att min bild inte riktigt hänger ihop men vid punkten B skulle alla linjer mötas på samma ställe.)
Det man skall upptäcka är att triangeln med sidorna c och d har vinkeln B och triangeln med sidorna d och e har vinkeln A. Man skall också inse att vinkeln A = vinkeln B.
Då börjar det roliga.
tan (A) = d/e
tan (B) = c/d
Eftersom A = B är tan (A) = tan (B) och då är
d/e = c/d
d = 75/2
c = 45 - 30 = 15
e = radien - c
75/2e = 15*2 / 75
e = 93,75
radien = 93,75 + 15 = 108,74
Vilket råkar vara dubbelt så mycket som 54,4.
En av våra uträkningar är då fel, jag tror naturligtvis på min.
Medlem
· Västra Götaland
· 231 inlägg
Tack för det snabba svaret.
Hittade lite mer formler:
Cirkel - Geometri - Plan figurer - Matematik minimum - Terminologi och begreppsförklaring
Hittade lite mer formler:
Cirkel - Geometri - Plan figurer - Matematik minimum - Terminologi och begreppsförklaring
Medlem
· Västra Götaland
· 231 inlägg
Det får vi nog skylla på min dåliga skiss. Den nya, något bättre bilden med rätt proportioner visar att korda-formlen nog är rätt.Mellanbarn skrev:
Kul formel det där. Har aldrig sett den förr men ska försöka lägga den i minnet.
Att inte lita på skisser lärde jag mig av en lärare på gymnasiet som visade en uppgift på tavlan.
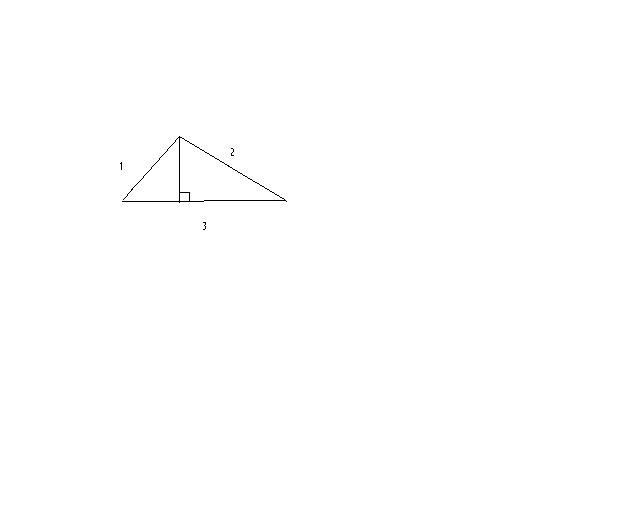
Uppgiften bestod i att räkna ut höjden på denna triangel. Men då skissen är helt upp åt väggarna för att det inte går att rita en triangel med sidorna 1,2 och 3 så blir självklart höjden lika med noll.
Att inte lita på skisser lärde jag mig av en lärare på gymnasiet som visade en uppgift på tavlan.
Uppgiften bestod i att räkna ut höjden på denna triangel. Men då skissen är helt upp åt väggarna för att det inte går att rita en triangel med sidorna 1,2 och 3 så blir självklart höjden lika med noll.
Jag undrar lite var Mellanbarn fick det ifrån att de båda trianglarna skulle vara likformiga om den långa kateten i den stora triangeln var just cirkelns radie. Det verkar ju vara så att de är likformiga om den sidan utgör diametern på cirkeln.
Nej, dom är ju inte likformiga om man tänker efter.jon_h skrev:
Min vinkel B är bara hälften av vinkeln A. Tur att min mattelärare inte ser detta.
Måste räkna om och se hur halva vinkeln kan ge halva svaret. Får tacka mattiaswahlberg för en bra sida.
Klicka här för att svara
Liknande trådar
-
Bygga 6m korsnich. Tips på med metod och material.
Möbelsnickeri -
App som mäter momentan elförbrukning/export till HAN-porten
Villalarm & Hemautomation -
Mura igen öppning och ansluta kamin, moment och material?
Värme allmänt -
Hetaste kökstrenderna 2025 – från naturmaterial till lyxig minimalism
Artikelkommentarer -
Vad är materialet och var kan man köpa det (i Sverige)
Badrum