Jag håller på att räkna på en ny altan och använder mig av denna
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
På sidan 19 står att golvbjälkarnas centrumavståndet ska vara högst plintavstånd/4. Det innebär alltså att om jag sätter fler plintar (minskar plintavståndet) så ska jag även lägga golvbjälkarna tätare. Varför då? Det känns ologiskt tycker jag!
I mitt fall har jag tänkt ha 2,15 mellan plintar på fri längd 3,1m och 45x220 bärlina. Ok enligt sidan 19. Jag är dock redan låst till cc 60 pga en tidigare konstruktion, vilket enligt sidan 19 är för mycket (bör vara max 2,15/4 = 53,75cm). För att komma upp i cc 60 ska jag alltså ha 2,4m mellan plintarna, vilket kräver 70x220 reglar....
Men scrollar jag ner lite till sida 25; dimensionering av golvbjälkar, så är min fria längd alltså 3,1 m vilket för cc60 kräver 45x120 C24. Ja men dåså, då är jag safe med mina cc60 trots allt? Eller?
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
På sidan 19 står att golvbjälkarnas centrumavståndet ska vara högst plintavstånd/4. Det innebär alltså att om jag sätter fler plintar (minskar plintavståndet) så ska jag även lägga golvbjälkarna tätare. Varför då? Det känns ologiskt tycker jag!
I mitt fall har jag tänkt ha 2,15 mellan plintar på fri längd 3,1m och 45x220 bärlina. Ok enligt sidan 19. Jag är dock redan låst till cc 60 pga en tidigare konstruktion, vilket enligt sidan 19 är för mycket (bör vara max 2,15/4 = 53,75cm). För att komma upp i cc 60 ska jag alltså ha 2,4m mellan plintarna, vilket kräver 70x220 reglar....
Men scrollar jag ner lite till sida 25; dimensionering av golvbjälkar, så är min fria längd alltså 3,1 m vilket för cc60 kräver 45x120 C24. Ja men dåså, då är jag safe med mina cc60 trots allt? Eller?
De vill bara ha marginal för att du inte ska belasta bärlinorna för mycket och få en ofördelaktig placering för lång ifrån ett upplag. längre ifrån ett upplag ger större moment på bärlinan och mer eller större nedböjning vid kritiskt läge som då blir mittemellan plintarna. därför vill de dra in c/c på golvbjälkarna till avstånd plint/4.
Du kan lägga på c/c 600 då 537 mm inte ger så mycket i sammanhanget, du kan få en större nedböjning än normalt (läs 5 mm vid max belastning). de bör ha räknat med 50kg eller 491N/m2 i bundenlast samt 2kN/m2 (203kg) i frilast och då kan du konstatera hur mycket du kommer att belasta golvet och du kommer aldrig upp i 203 kg/m2 möbler samt personer så du kan med andra ord sova lungt. Ställ inte dit flygeln eller ett 500kg betongbord bara.
sista kommentaren om sid 25 handlar inte om bärlinan i detta fallet utan bara om bjälkarna.
De utgår från att din bärlina klarar allt du belastar den med och utgår bara från golvbjälkarna.
anledningen till sidan 19 är att de tar hänsyn till moment i bärlinan samt att de vill få upplag från plintarna.
Du kan lägga på c/c 600 då 537 mm inte ger så mycket i sammanhanget, du kan få en större nedböjning än normalt (läs 5 mm vid max belastning). de bör ha räknat med 50kg eller 491N/m2 i bundenlast samt 2kN/m2 (203kg) i frilast och då kan du konstatera hur mycket du kommer att belasta golvet och du kommer aldrig upp i 203 kg/m2 möbler samt personer så du kan med andra ord sova lungt. Ställ inte dit flygeln eller ett 500kg betongbord bara.
sista kommentaren om sid 25 handlar inte om bärlinan i detta fallet utan bara om bjälkarna.
De utgår från att din bärlina klarar allt du belastar den med och utgår bara från golvbjälkarna.
anledningen till sidan 19 är att de tar hänsyn till moment i bärlinan samt att de vill få upplag från plintarna.
Ok, så D/4 syftar till att säkerställa att last alltid fördelas på ett visst antal (4) punkter över bärlinan.
Om vi tar exemplet d=2,4m och cc600, vi har fyra reglar som belastar en bärlina mellan två plintar. Om jag minskar d till t ex 2m innebär det att bara tre reglar hamnar inom d och således färre punkter som en given last fördelas på. Förstår jag det rätt då?
Ekvationen måste väl dock hänga ihop med dimensionen på bärlinan? Eftersom momentet minskar parallellt med d så tål ju en given bärlina mer last med minskat d.
Alltså: Eftersom jag är låst vid cc60 så bör jag dimensionera bärlinan utifrån antagandet d=2,4. Givet att jag inte går ner i dimension på bärlinan kan jag då utan risk minska d (ju mer desto stabilare konstruktion).
Tänker jag rätt? Jag har inte tänkt ställa en flygel på, men jag kan inte garantera att det aldrig kommer ställas ut en pool, så jag vill inte fuska med konstruktionen.
Förresten; Bonusfråga på bärkraft: Lathunden säger att trallen ska va minst 22mm tjock, men gör ingen skillnad på t ex 28 eller 34. Jag väljer mellan 28x145 och 34x145 och förstår att den senare blir stummare, men det är inget berg jag konstruerar så lite (i princip okännbar) svikt är ok. Men bör valet påverka dimensioneringen av reglar på något sätt?
Om vi tar exemplet d=2,4m och cc600, vi har fyra reglar som belastar en bärlina mellan två plintar. Om jag minskar d till t ex 2m innebär det att bara tre reglar hamnar inom d och således färre punkter som en given last fördelas på. Förstår jag det rätt då?
Ekvationen måste väl dock hänga ihop med dimensionen på bärlinan? Eftersom momentet minskar parallellt med d så tål ju en given bärlina mer last med minskat d.
Alltså: Eftersom jag är låst vid cc60 så bör jag dimensionera bärlinan utifrån antagandet d=2,4. Givet att jag inte går ner i dimension på bärlinan kan jag då utan risk minska d (ju mer desto stabilare konstruktion).
Tänker jag rätt? Jag har inte tänkt ställa en flygel på, men jag kan inte garantera att det aldrig kommer ställas ut en pool, så jag vill inte fuska med konstruktionen.
Förresten; Bonusfråga på bärkraft: Lathunden säger att trallen ska va minst 22mm tjock, men gör ingen skillnad på t ex 28 eller 34. Jag väljer mellan 28x145 och 34x145 och förstår att den senare blir stummare, men det är inget berg jag konstruerar så lite (i princip okännbar) svikt är ok. Men bör valet påverka dimensioneringen av reglar på något sätt?
Helt rätt att de vill fördela på 4 punkter i sin tabell över dim på bärlinor, annars blir deras tabell jätte stor och får inte plats i fickformat.
Vill du ha 2,4 meter mellan plintarna och uppfylla kraven för c/c 600mm får du gå upp på limträ eller annan typ av balk då de bara har med upp till 220 höga K24 bärlinor i sin tabell.
se sidan 20 för limträ balkar, men du får gräva djupare för samma höjd.
gällande bonusfrågan är det så att man börjar dim från där man har lasten dvs golvet, då tar man och kontrollerar tjocklek mot c/c på golvbjälkar och sen mot bärlina och bärlina mot plint upplagen och sen plintar mot marken. har du längre c/c än 600 bör man öka till 28 eller 34.
Allt handlar om nedböjning som är acceptabel. du vill inte att golvet ska luta 1 cm mellan reglarna om man står mitt mellan. det får man om man har för långt mellan eller för låg konstruktion på golvet, prova med en bärda 22 mm, ställ dig mitt på den med upplag c/c 400, 600, 800 och 1000 och du kommer få olika nedböjning på mitten. det samma gällar för bärlinan bara att den tar upp last från fler golvbjälkar och större yta av golvet.
hoppas jag är tydlig det är inte lätt utan att rita ibland.
Vill du ha 2,4 meter mellan plintarna och uppfylla kraven för c/c 600mm får du gå upp på limträ eller annan typ av balk då de bara har med upp till 220 höga K24 bärlinor i sin tabell.
se sidan 20 för limträ balkar, men du får gräva djupare för samma höjd.
gällande bonusfrågan är det så att man börjar dim från där man har lasten dvs golvet, då tar man och kontrollerar tjocklek mot c/c på golvbjälkar och sen mot bärlina och bärlina mot plint upplagen och sen plintar mot marken. har du längre c/c än 600 bör man öka till 28 eller 34.
Allt handlar om nedböjning som är acceptabel. du vill inte att golvet ska luta 1 cm mellan reglarna om man står mitt mellan. det får man om man har för långt mellan eller för låg konstruktion på golvet, prova med en bärda 22 mm, ställ dig mitt på den med upplag c/c 400, 600, 800 och 1000 och du kommer få olika nedböjning på mitten. det samma gällar för bärlinan bara att den tar upp last från fler golvbjälkar och större yta av golvet.
hoppas jag är tydlig det är inte lätt utan att rita ibland.
Jag funderade på det här ett par vändor till. Det går att få 3 punkter om golvreglarna ligger precis på plintarna. Och eftersom den enda anledningen jag kan komma på till att cc mellan golvreglar ska minska parallellt med avstånd mellan plintar är att undvika att lasten fördelas på för få punkter så borde ekvationen vara i steg/intervall snarare än linjärt.
Exempel: d=2m -> cc 50 cm. Det sämsta för bärlinan och en given last är då om golvreglarna ligger precis på plinten, eftersom vi då bara har tre punkter som belastar bärlinan. Om jag nu minskar d till 1,9....1,8....1,7...1,6... så förändras ingenting förutom att momentet mot plintarna minskar (bärlinans bärförmåga ökar) eftersom det fortfarande inte kan bli mindre än 3 golvreglar mellan två plintar. Vid d = 1,5 däremot uppstår läget att det kan bli 2 punkter och den lokala kraften mot bärlinan ökar (givet ogynnsam placering av last).
Alltså borde riktlinjen vara att cc ska vara mellan d/4 och d/3, och mina cc 600 på d=2,15 är med andra ord helt okej
Med reservation för att jag helt missat poängen
Exempel: d=2m -> cc 50 cm. Det sämsta för bärlinan och en given last är då om golvreglarna ligger precis på plinten, eftersom vi då bara har tre punkter som belastar bärlinan. Om jag nu minskar d till 1,9....1,8....1,7...1,6... så förändras ingenting förutom att momentet mot plintarna minskar (bärlinans bärförmåga ökar) eftersom det fortfarande inte kan bli mindre än 3 golvreglar mellan två plintar. Vid d = 1,5 däremot uppstår läget att det kan bli 2 punkter och den lokala kraften mot bärlinan ökar (givet ogynnsam placering av last).
Alltså borde riktlinjen vara att cc ska vara mellan d/4 och d/3, och mina cc 600 på d=2,15 är med andra ord helt okej
Med reservation för att jag helt missat poängen
Nej, ligger en last rakt ovanför plinten blir det inget moment i bärlinan för den alls, dvs moment av 3 laster istället för 4 som du får vid upplag när plinten är mitt mellan 2 golvreglar.
Moment är en rörelse och när du stoppar rörelsen får du en nedböjning. kraften från golvbjälkarna skapar moment i bärlinan. (se fig gick inte att hålla sig ifrån att rita)
Så de har D/4 för att vara säker att du ska klara dig.
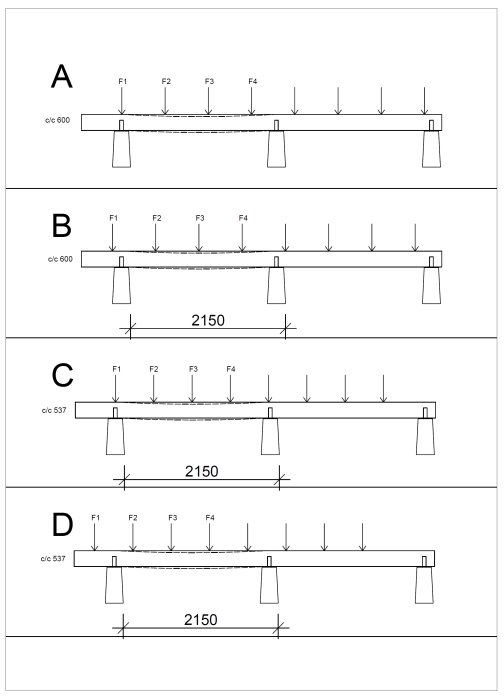
Kommentar till figur,
I A och B har jag c/c 600 som du vill ha, A är rak över plint och B är sämsta fallet man kan få med last mittmellan plintar dvs längsta avståndet till upplag (blir största momentet exponentiellt då man tar kraft gånger avstånd)
I C och D är c/c minskat till D/4 537 mm, detta ger då en lägre last per F1 - F4 jämfört med A och B. då varje golvbjälke ska i A och B ta upp 0,6x1,55x2kN och i C och D 0,537x1,55x2kN
A och B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C och D för F1 - F4 = 1,66 + ,5kN = 2,16 kN
Skillnad 2,36-2,16 = 0,2kN eller c:a 10% mer i A och B.
När du får sämsta läget på båda hamnar du mitt mellan upplagen dvs 2,15/2 = 1,075 m gånga detta med tidigare resultat och du får 2,53kNm för A och B samt 2,32 kNm för C och D.
Dvs C och D kommer att ha mindre moment än A och B.
Till sist kan jag hålla med om att de använder ett trubbig siffra för att kalkylera rätt cc avstånd, men att lägga med en kurva att läsa av för att dela olika d med 3,5 till 4,5 i en exponentiell kurva hade bara varit krångligt.
Moment är en rörelse och när du stoppar rörelsen får du en nedböjning. kraften från golvbjälkarna skapar moment i bärlinan. (se fig gick inte att hålla sig ifrån att rita)
Så de har D/4 för att vara säker att du ska klara dig.
Kommentar till figur,
I A och B har jag c/c 600 som du vill ha, A är rak över plint och B är sämsta fallet man kan få med last mittmellan plintar dvs längsta avståndet till upplag (blir största momentet exponentiellt då man tar kraft gånger avstånd)
I C och D är c/c minskat till D/4 537 mm, detta ger då en lägre last per F1 - F4 jämfört med A och B. då varje golvbjälke ska i A och B ta upp 0,6x1,55x2kN och i C och D 0,537x1,55x2kN
A och B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C och D för F1 - F4 = 1,66 + ,5kN = 2,16 kN
Skillnad 2,36-2,16 = 0,2kN eller c:a 10% mer i A och B.
När du får sämsta läget på båda hamnar du mitt mellan upplagen dvs 2,15/2 = 1,075 m gånga detta med tidigare resultat och du får 2,53kNm för A och B samt 2,32 kNm för C och D.
Dvs C och D kommer att ha mindre moment än A och B.
Till sist kan jag hålla med om att de använder ett trubbig siffra för att kalkylera rätt cc avstånd, men att lägga med en kurva att läsa av för att dela olika d med 3,5 till 4,5 i en exponentiell kurva hade bara varit krångligt.
Klicka här för att svara