Beräkna fasström, osymmetrisk last

[bortan]

Är nyfiken på hur man beräknar fasström för en osymmetrisk last. Vad blir strömmen i L3 i nedanstående krets:


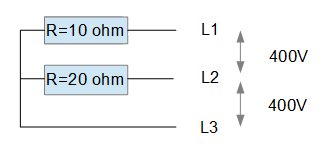
L1 och L2 är enkelt eftersom man får 400V över resistanserna:
L1=400V/10ohm=40A
L2=400V/20ohm=20A
L3=?

Det går att räkna ut detta m.h.a visardiagram, men jag undrar hur den matematiska formeln ser ut?
Givet att faserna är förskjutna 120 grader inbördes.

 

[Millox]

Du får komplexsummera:
I1 = 400*exp(j*w)/10;
I2 = 400*exp(j*w+2.*pi.*j/3)20;

I3 = I1+I2

Det blir 34 A

 

[bortan]

Tack för svaret!

Dina beräkningar av I1 och I2 är egentligen bara underlag för att räkna ut I3?

Har jag förstått det rätt att det är såhär man ska räkna:
I1= 400/10
I2= 400/20
I3= (400*exp(j*w)/10)+(400*exp(j*w+2.*pi.*j/3)20)

Kommer "j" och "w" i dina formler från j omega metoden?

 

[Bo.Siltberg]

Din sista formel är ju lika med I1+I2 om du använder rätt fasvinklar för dessa två. Att strömmen i I1 eller I2 har en viss fasvinkel påverkar inte deras absolutbelopp var för sig. Men om man summerar dem så kommer fasvinkeln in i bilden.

Och ja, det är jw-metoden som Millox visar, absolutbelopp och dess fasvinkel. Om du vill räkna mha "grundläggande" matte skulle jag rekommendera ett visardiagram där du använder cosinus och Pythagoras.

 

[Bo.Siltberg]

Fast det ska vara I1-I2 för att värdet på strömmen I3 ska bli rätt, 53 A. Pilarna för strömmar mellan faserna bli vända mot varandra.

 

[bortan]

Ok, då tror jag att jag hänger med, tack så mycket för all hjälp!

Med enklare matte, som du tipsar om Bo, blir formeln såhär om jag förstått det rätt:

I3= "roten ur" I1^2 + I2^2 - 2 * I1 * I2 * cos120

 

[Bo.Siltberg]

Ja där fick du till det med Cosinussatsen i all sin glory om vi antar att I1 och I2 är reella tal utan någon fasvinkel.