Vad händer vid alldeles för högt flöde i radiatorn?
Jag har en allmän fundering...
De flesta värmesystem vill ha ett visst flöde och delta-t över radiatorerna av olika skäl.
Men om vi bortser från det och endast fokuserar på atr värma upp ett rum så snabbt som möjligt.
I min värld borde det gå snabbast att värma upp rummet med så högt flöde som möjligt i radiatorn. Men då sjunker delta-t över radiatorn och enligt formeln nedan avger den ingen värme.
P=F×Cp×(Tin-Tut)
Om Tin=Tut så avger radiatorn ingen värme alls, men så länge rummet är kallare än radiatorn måste den avge värme till rummet enligt fysiklagarna, så dt kan inte vara noll...
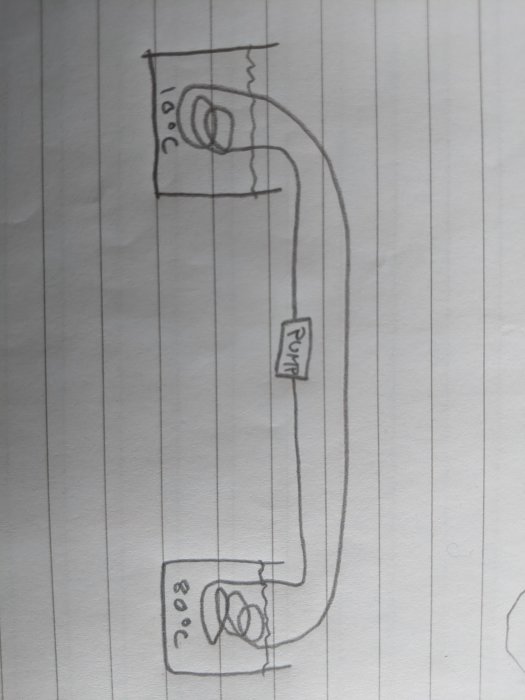
Ett annat sätt att se det på: Ponera två 1m3-tankar där den ena är fylld med 80-gradigt vatten och den andra 10-gradigt vatten. I varje tank finns en spiral (likt en VV-beredarslinga) och en pump som kan pumpa vätska genom spiralerna. Hur fort ska pumpen gå för att så snabbt som möjligt jämna ut temperaturskillnaden mellan de två tankarna?
De flesta värmesystem vill ha ett visst flöde och delta-t över radiatorerna av olika skäl.
Men om vi bortser från det och endast fokuserar på atr värma upp ett rum så snabbt som möjligt.
I min värld borde det gå snabbast att värma upp rummet med så högt flöde som möjligt i radiatorn. Men då sjunker delta-t över radiatorn och enligt formeln nedan avger den ingen värme.
P=F×Cp×(Tin-Tut)
Om Tin=Tut så avger radiatorn ingen värme alls, men så länge rummet är kallare än radiatorn måste den avge värme till rummet enligt fysiklagarna, så dt kan inte vara noll...
Ett annat sätt att se det på: Ponera två 1m3-tankar där den ena är fylld med 80-gradigt vatten och den andra 10-gradigt vatten. I varje tank finns en spiral (likt en VV-beredarslinga) och en pump som kan pumpa vätska genom spiralerna. Hur fort ska pumpen gå för att så snabbt som möjligt jämna ut temperaturskillnaden mellan de två tankarna?
Det kräver ju oändligt flöde och leder till en uträkning av typen "vad blir produkten av något som går mot noll gånger något som går mot oändligheten".
Effekten av radiatorn beror på dess logaritmiska medeltemperatur. Vid ett flöde som går mot oändligheten blir den samma som temperaturen in och det är också då du får ut max effekt. (Givet en konstant tilloppstemperatur varmare än rumstemperaturen.)
Effekten av radiatorn beror på dess logaritmiska medeltemperatur. Vid ett flöde som går mot oändligheten blir den samma som temperaturen in och det är också då du får ut max effekt. (Givet en konstant tilloppstemperatur varmare än rumstemperaturen.)
Jag är rädd för du har missförstått hur ett värmeelement(radiator) vid vattenburen värme fungerar.
Den temperaturskillnad som driver värmeöverföring från radiatorn till rummet, är radiatorns medel-yttemperatur minus rummets lufttemperatur. Ju större skillnad mellan dessa temperaturer desto större avgiven effekt från radiatorn.
Genom att ha stort varmvattenflöde genom en radiatorn kan yttemperaturen hållas hög även nära radiatorns vattenutlopp. Med en liten radiator kan man då få hög avgiven värmeeffekt.
Men det kostar elektrisk energi för en cirkulationpump att pumpa runt en massa vatten på det sättet. Det skulle nog även susa och brusa i radiatorn(icke önskvärt i t.ex. sovrum). Istället monteras en överdimensionerad radiator så att den kan klara värmebehovet utan att behöva ha högt vattenflöde.
Exempel 1 kW avgiven effekt
P = F x Cp x (Tin-Tut) = 7,94 kg/s x 4,2 kJ/(kg Grad) x (60 - 30) = 1000 W
Men samma avgivna effekt fås om flödet ökat 10 gånger och utloppstemp = 57 grader om:
P = F x Cp x (Tin-Tut) = 79,4 kg/s x 4,2 kJ/(kg grader) x (60 - 57) = 1000 W
Där Tin = vatteninloppstemperatur på radiatorn.
Tut = vattenutloppstemperatur från radiatorn.
Den temperaturskillnad som driver värmeöverföring från radiatorn till rummet, är radiatorns medel-yttemperatur minus rummets lufttemperatur. Ju större skillnad mellan dessa temperaturer desto större avgiven effekt från radiatorn.
Genom att ha stort varmvattenflöde genom en radiatorn kan yttemperaturen hållas hög även nära radiatorns vattenutlopp. Med en liten radiator kan man då få hög avgiven värmeeffekt.
Men det kostar elektrisk energi för en cirkulationpump att pumpa runt en massa vatten på det sättet. Det skulle nog även susa och brusa i radiatorn(icke önskvärt i t.ex. sovrum). Istället monteras en överdimensionerad radiator så att den kan klara värmebehovet utan att behöva ha högt vattenflöde.
Exempel 1 kW avgiven effekt
P = F x Cp x (Tin-Tut) = 7,94 kg/s x 4,2 kJ/(kg Grad) x (60 - 30) = 1000 W
Men samma avgivna effekt fås om flödet ökat 10 gånger och utloppstemp = 57 grader om:
P = F x Cp x (Tin-Tut) = 79,4 kg/s x 4,2 kJ/(kg grader) x (60 - 57) = 1000 W
Där Tin = vatteninloppstemperatur på radiatorn.
Tut = vattenutloppstemperatur från radiatorn.
Redigerat:
En annan nackdel med ett högt flöde är att vattnet som flödar genom radiatorn kommer från någon form av ackumulatortank, som i normalfallet har varmt vatten överst och kallt underst. Vid ett högt flöde kommer den skiktningen fallera, vilket kommer sänka ditt Tin (och därmed ditt Tut).
Men, i en ideal värld med en oändlig mängd varmvatten och inga pumpförluster skulle du få högst effekt med ett oändligt flöde.
Men, i en ideal värld med en oändlig mängd varmvatten och inga pumpförluster skulle du få högst effekt med ett oändligt flöde.
Precis som du säger är det väl skillnaden mellan radiatorns temperatur och omgivande luft som driver värmeöverföringen.A Arnodt skrev:
Anledningen till min fråga är att någon sade "har du ingen diff mellan in och retur så får du inte ut någon värme och din panna behöver aldrig jobba" vilket jag påstår är ett direkt felaktigt påstående.
Vad är det som säger att delta-t blir en tiondel när flödet ökar en faktor 10? Vid lägre delta-t ökar ju radiatorns ytmedeltemperatur och därmed borde den avgivna värmeeffekten bli högre.
Sus och brus och cirkulstionspumpar bryr jag mig inte om i detta fall, utan är endast intresserad av att teoretiskt värma upp ett rum så snabbt som möjligt/få ut maximal effekt ur en radiator.
Om du tittar litet noggrannare, så angav jag i båda exemplen en viss bestämd avgiven effekt, nämligen just 1,0 kW. Inget sades om rummets temperatur, utan endast radiatorn betraktades. Då flödet var 10 gånger högre(temperaturdifferensen på radiatorvattnet in/ut, en tiondel), var rummets temperatur också högre, såvida det var samma radiator, just så mycket högre att det blev 1 kW avgiven värme från radiatorn. Ökar du lufttemperaturen i rummet minskar ju avgiven värme från radiatorn. Om luften i rummet har samma temperatur som radiatorns yttemperatur, avstannar värmeöverföringen helt och hållet.
Påståendet "har du ingen diff mellan in och retur så får du inte ut någon värme och din panna behöver aldrig jobba" vilket jag påstår är ett direkt felaktigt påstående.
Det påståendet stämmer faktiskt.
Är temperaturen på rumsluften lägre än radiatorvattnets inloppstemperatur, får du tvungetvis avgiven värme från radiatorn, och följdaktligen är radiatorvattnet kallare ut än in. Har man oerhört högt vattenflöde, ca 100 gånger högre än normalt, då kanske man mäter radiatorutloppstempen till 59,5 grader och inloppstemp till 60 grader. Det är likväl en temperaturskillnad, om än väldigt liten, och det blir en betydande avgiven effekt likväl pga det höga vattenflödet. Men jag tror en vanlig cirkulationspump för radiatorvatten kan endast klara lågt pumpflöde, är de ofta bara på ca 100 W.
Påståendet "har du ingen diff mellan in och retur så får du inte ut någon värme och din panna behöver aldrig jobba" vilket jag påstår är ett direkt felaktigt påstående.
Det påståendet stämmer faktiskt.
Är temperaturen på rumsluften lägre än radiatorvattnets inloppstemperatur, får du tvungetvis avgiven värme från radiatorn, och följdaktligen är radiatorvattnet kallare ut än in. Har man oerhört högt vattenflöde, ca 100 gånger högre än normalt, då kanske man mäter radiatorutloppstempen till 59,5 grader och inloppstemp till 60 grader. Det är likväl en temperaturskillnad, om än väldigt liten, och det blir en betydande avgiven effekt likväl pga det höga vattenflödet. Men jag tror en vanlig cirkulationspump för radiatorvatten kan endast klara lågt pumpflöde, är de ofta bara på ca 100 W.
Redigerat:
A Arnodt skrev:
P PatrikJo skrev:
Tack. Ett tag började jag fundera på om jag var helt dum i huvudet och glömt den grundläggande termodynamiken.A Arnodt skrev:
Edit: Än kvarstår att lära sig citera korrekt på byggahus....
Påståendet om att vid noll differens så går noll energi till rummet är korrekt, men du tänker åt fel håll. Enda gången du kan ha noll delta-T är om rummet är lika varmt som radiatorn. Annars kommer du alltid ha en delta-T, om än liten.
Du verkar ju ha det klart för dig och med det Arnodt skriver kan du då se det som någon sagt som felaktigt i de flesta praktiska fall. Dvs varmare vatten in i radiatorn än rumstempen då får du givetvis mer effekt vid lägre delta och högre flöde. Och ska du vara mer finstilt får du som Bigfoot skrev i #2 använda logaritmiska medeltemperaturer men det duger bra med rena medel in/ut på vattnet och rumstempen på andra sidan.D daniel_021 skrev:
Det som kan vara mer intressant är att se på hur en förändring i framtemp ställer sig mot ökad pumpning för större flöde. I ena fallet direkt proportionellt och i andra förluster och ökad pumpeffekt mot både kvadrat och kub lite som resonemangen bakom högspänd elkraftöverföring.
Det är andra aspeketer på detta också. Har du hög vattentemperatur ut radiatorn, säg 60 grader och du har en värmepump som är den som sedan ska värma vattnet till radiatorn igen. För att den ska ytterligare kunna värme ett redan hett vatten på ca 60 grader måste den jobba hårdare, och tvingas att jobbar med dålig verkningsgrad dvs drar mer ström. Får värmepumpen istället kallare returvatten, säg 30 grader, då har den enklare jobb upp till 60 grader att värma. Rörmokaren kanske vet hur det ska vara, men kanske inte teorierna varför. Liksom den som kör en moped inte behöver känna till alla teorierna om förbränning och värmeöverföring och omvandling till mekanisk energi, han kör lika bra ändå.
Redigerat: