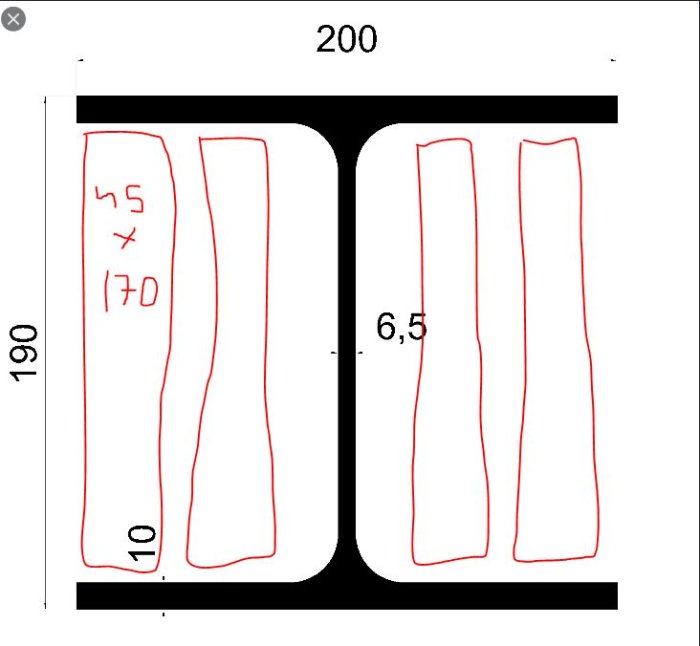
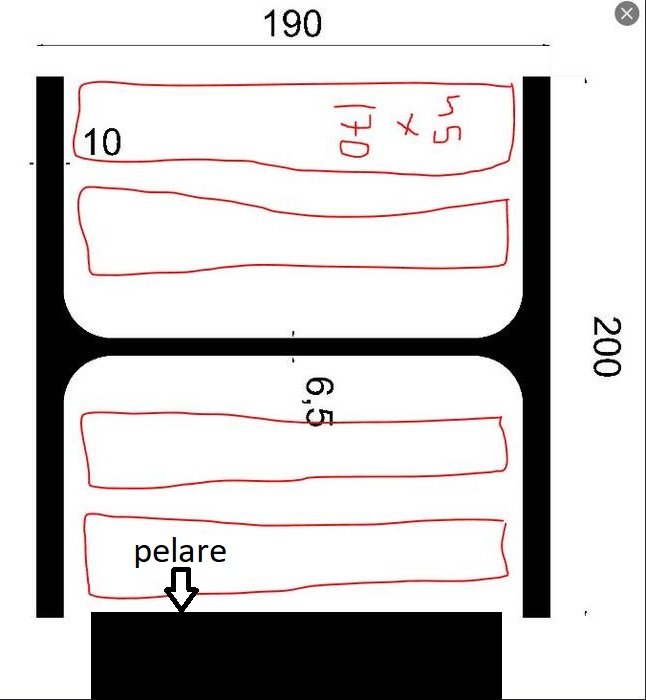
Fylling med tre gir i stor grad ingenting i stivhet. Ved samme deformasjon vil i stor grad all last bli tatt opp av stålbjelken, som materialmessig har ca 40 ganger større stivhet enn tre. Som tankeeksperiment: legg en gummistrikk på en stållinjal og utsett sandwichen for strekkbelastning. Hvilket materiale tar hoveddelen av lasten?
Om du overhodet skal få noen hjelp av trelektene så må de samvirke med stålbjelken, dvs være "koblet" til hverandre og ikke bare "inkilt". Nå er det veldig stor forskjell mellom styrkene til stål og tre, så det eventuelle tilskuddet her er nok å betrakte som ubetydelig.
Hvordan mener du med koblet?R roli skrev:
tja man kan jo leke med tanken at det blir stivere MEN når bjelken brister er det en sånn kraft så det ikke spiller noen rolle hva slags dimensjon elr antall planker imellom .... MEN er jo nå spekulert på verste tenkbare scenario at det klippes av på en gang ^^
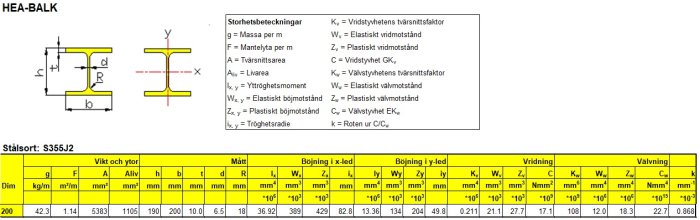
men min teori i min lille rosa verden at man må regne holdfastheten skilt for seg for bjelken (HEA fra størrelsen) og tre (C16 C24 C30) og så er spennvidden og belastningen som vil være med og leke ... så kan man være nitid med innfesting av trevirket... bruk av boltpistol hvor mye påvirker hullene i bjelken etc
finnes mye
men min teori i min lille rosa verden at man må regne holdfastheten skilt for seg for bjelken (HEA fra størrelsen) og tre (C16 C24 C30) og så er spennvidden og belastningen som vil være med og leke ... så kan man være nitid med innfesting av trevirket... bruk av boltpistol hvor mye påvirker hullene i bjelken etc
finnes mye
Nei. Dere tenker feil. Innfestingen av materialene i hverandre har en forsumbar betydning i dette tilfellet. Skulle det vært en sandwichkonstruksjon så er det viktig, men så er det ikke.
Nedbøyningen for en gitt geometri er direkte proporsjonal mot materialets E-modul. E-modulen er en materialkonstant for et materiales stivhet. Stål har ca 210 GPa og tre et sted rundt 5 GPa. Det er en forskjell på en faktor 40. Nå har riktig nok de forskjellige materialene forskjellige geometrier, men det har liten betydning for resonnementet. Om vi setter sammen tre med stål i henhold til den første skissen, så vil belastningen gi nøyaktig samme deformasjon, ikke sant? De sitter jo sammen. Spenningen i en belastet konstruksjon med en gitt deformasjon er direkte avhengig av E-modulen. Dette kalles Hookes lov. Det fører til at spenningen i stålet blir så mye høyere at det tar i stort sett hele lasten, og treet tar nesten ingen last i det hele tatt. Med så lav spenning i treet vil stivheten i den totale konstruksjonen knapt påvirkes i det hele tatt av at man legger inn tre.
Nedbøyningen for en gitt geometri er direkte proporsjonal mot materialets E-modul. E-modulen er en materialkonstant for et materiales stivhet. Stål har ca 210 GPa og tre et sted rundt 5 GPa. Det er en forskjell på en faktor 40. Nå har riktig nok de forskjellige materialene forskjellige geometrier, men det har liten betydning for resonnementet. Om vi setter sammen tre med stål i henhold til den første skissen, så vil belastningen gi nøyaktig samme deformasjon, ikke sant? De sitter jo sammen. Spenningen i en belastet konstruksjon med en gitt deformasjon er direkte avhengig av E-modulen. Dette kalles Hookes lov. Det fører til at spenningen i stålet blir så mye høyere at det tar i stort sett hele lasten, og treet tar nesten ingen last i det hele tatt. Med så lav spenning i treet vil stivheten i den totale konstruksjonen knapt påvirkes i det hele tatt av at man legger inn tre.
Sist redigert:
Klikk her for å svare