Hei alle,
har kjørt meg fast med et enkelt mekanikkspørsmål, sukk.
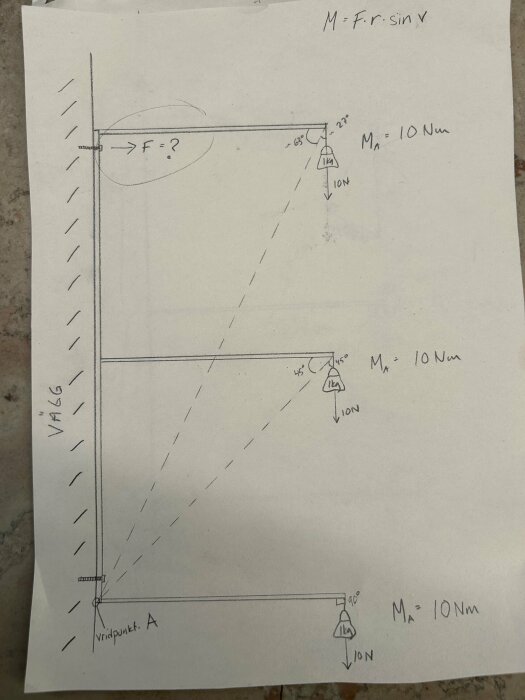
Jeg prøver å regne ut kraften som virker på den øvre innfestingen på en konsoll med tre plan. Altså kraften som vil dra ut skruen fra veggen når man belaster hylleplanene.
Jeg tenkte at man skulle regne ut vridningsmomentet i vridningspunktet (helt nederst på den delen av konsollen som ligger mot veggen)
Jeg forstår at det er mange andre krefter involvert, men antatt at konsollen er hengslet i det punktet. Ser bort fra den nedre skruen på bildet.
Jeg får det til at alle planene bidrar med samme vridningsmoment, kan det virkelig stemme? Regner jeg feil?
Hvordan ville dere regne ut kraften?
Mvh
Johan
har kjørt meg fast med et enkelt mekanikkspørsmål, sukk.
Jeg prøver å regne ut kraften som virker på den øvre innfestingen på en konsoll med tre plan. Altså kraften som vil dra ut skruen fra veggen når man belaster hylleplanene.
Jeg tenkte at man skulle regne ut vridningsmomentet i vridningspunktet (helt nederst på den delen av konsollen som ligger mot veggen)
Jeg forstår at det er mange andre krefter involvert, men antatt at konsollen er hengslet i det punktet. Ser bort fra den nedre skruen på bildet.
Jeg får det til at alle planene bidrar med samme vridningsmoment, kan det virkelig stemme? Regner jeg feil?
Hvordan ville dere regne ut kraften?
Mvh
Johan
Beste svar
Djevelen sitter i detaljene. Det er nettopp dette med "enkel mekanikkspørsmål" som noen ganger forenkler problemet mer enn man tenker seg. Hvis hyllen virkelig ser ut som skissen så vil ryggen være bøyelig. Dermed kan du få en større kraft på den øvre skruen ved belastning av øverste hylleplan. Er det derimot en hylle med sider så vil den ikke bøyes nevneverdig. Du har tenkt riktig med beregningen. Og så lenge hyllen er ganske stiv og sitter fast stemmer beregningen med praksis også.
R RiKr skrev:
Hei,A ArneTW skrev:
Takk for svaret!
Jeg forstår ikke hvordan du regner men vil gjerne forstå om du kanskje kan forklare nærmere, vise?
Mvh
Johan
ta hver hylle for seg...Attefallshuset skrev:
Jeg antar at hver hylle er 1m og avstanden mellom er 1m også.
regn moment rundt ditt punkt A.
Hylle nederst
1m * 10N = 2m x XN, X=5N
hylle2
(1m+1m)*10N=2m*XN, X=10N
hylle3
(1m+1m+1m)*10N=2m*XN, X=15N
adder til 30N.
At hyllene er 90° utad spiller ingen rolle... Du kan like gjerne tenke at de står rett opp.
jeg ignorerer all egenvekt etc og også skjøt- og friksjonskrefter, og alt er 100% stivt.
/ATW
Det blir jo andre krefter også... skjærkraften. dvs en kraft vertikalt ned langs veggen.T topmount skrev:
30N om det er en skrue, men om man regner med 2 skruer blir det en verdi mellom 0 og 30N.
Så kommer friksjon osv.
Man kan komplisere det..
Jeg oppfattet at TS spurte etter kraftkomponenten som vil rive skruen ut av veggen...
/ATW
Det er jo den projiserte avstanden mellom tyngde og vrispunktet A som er interessant. Og det er det samme for alle hylleplan Hva er det du legger til? Jeg hevder at alle tre tyngderne bidrar med 10 Nm rundt A akkurat som @Attefallshuset skrevet på sin skisse. Og følgelig sammenlagt 15 N trekkraft i skruens retning.A ArneTW skrev:
Jeg synes du tar feil... Den vertikale posisjonen av hylleplanene spiller en rolle ifølge meg.A Avemo skrev:
Dvs om du legger til et hylleplan som ligger 1000m opp, ville du fått et skikkelig tillegg og ikke bare 5N til...
Du får 10Nm ved hvert hylleplansfeste men du kan ikke bare flytte det ned til A.
/ATW
I TS teoretiske og statiske modell der "vridpunkt A" er et leddet støtte, er det slik. I virkeligheten er det så klart mer komplisert, men hvis man har tenkt riktig, fanger modellen det som er relevant.T topmount skrev:
Hobbyelektriker
· Värmland, Molkom
· 26 137 innlegg
Hva var svaret, dvs hvordan resonerer man for å komme fram til løsningen?
Først regner man ut hvor stort dreiemoment de respektive hylleplanene bidrar med i punkt A.
Kun den kraftkomponenten som er vinkelrett mot spaken bidrar til dreiemomentet. Dvs. når du drar i en skiftenøkkel er det kun den kraften som appliseres i "rotasjonsretningen" som skaper dreiemoment.
Ut fra dette kan man enkelt avgjøre dreiemomentet det nederste hylleplanet bidrar med fordi denne kraften i sin helhet er vinkelrett mot spaken (hylleplanet). Dreiemomentet = kraften × spakens lengde: τ = Fr.
TS har kraften 10 N og kommer åpenbart fram til 10 Nm, noe som gjør at vi kan slutte oss til at hylleplanets lengde er 1 m.
For hylleplan to tenker TS seg at vinkelen rygg og hylleplan danner en imaginær spak fra punkt A til punktet hvor kraften angriper. Kraften angriper dog da ikke vinkelrett mot den imaginære spaken, og TS må derfor regne ut den kraftkomponenten som er vinkelrett mot denne, hvilket er F⊥= |F| sin θ, der F er kraften og θ er vinkelen relativt til spaken. Vinkelen er i dette tilfelle 45°, så F⊥ = 10 × sin 45° = 10 × √2 / 2 = 5 × √2.
Vinkelen 45° avslører også at avstanden til hylleplan to = 1 m. Lengden på den imaginære spaken gis av pytagoras’ læresetning: c = √(a² + b²) = √(1² + 1²) = √2.
Man kan nå regne ut dreiemomentet som hylleplan to bidrar med: τ = Fr = 5 × √2 × √2 = 5 × √2² = 5 × 2 = 10 Nm.
Den observante noterer her sammenhengen mellom kraftvektoren og den imaginære spakens lengde og innser at avstanden mellom hyllene kan elimineres fra ligningen. Alle hylleplan bidrar med samme dreiemoment uansett høyde.
Det samlede dreiemomentet kan derfor enkelt bestemmes til 3 × 1 × 10 = 30 Nm.
For å deretter regne ut kraften F når dreiemomentet er kjent får vi regne baklengs:
τ = Fr → 30 = F × 2 → F = 30 / 2 = 15 N.