Jeg holder på å regne på en ny terrasse og bruker denne
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
På side 19 står det at senteravstanden for gulvbjelkene skal være høyest pilaravstand/4. Det betyr altså at om jeg setter flere pilarer (reduserer pilaravstanden) så skal jeg også legge gulvbjelkene tettere. Hvorfor det? Det føles ulogisk synes jeg!
I mitt tilfelle har jeg tenkt å ha 2,15 mellom pilarer på fri lengde 3,1 m og 45x220 bærebjelke. Ok ifølge side 19. Jeg er dog allerede låst til cc 60 på grunn av en tidligere konstruksjon, hvilket ifølge side 19 er for mye (bør være maks 2,15/4 = 53,75 cm). For å komme opp i cc 60 skal jeg altså ha 2,4 m mellom pilarene, hvilket krever 70x220 bjelker....
Men blar jeg litt ned til side 25; dimensjonering av gulvbjelker, så er min frie lengde altså 3,1 m hvilket for cc60 krever 45x120 C24. Ja, men da så, da er jeg trygg med mine cc60 tross alt? Eller?
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
På side 19 står det at senteravstanden for gulvbjelkene skal være høyest pilaravstand/4. Det betyr altså at om jeg setter flere pilarer (reduserer pilaravstanden) så skal jeg også legge gulvbjelkene tettere. Hvorfor det? Det føles ulogisk synes jeg!
I mitt tilfelle har jeg tenkt å ha 2,15 mellom pilarer på fri lengde 3,1 m og 45x220 bærebjelke. Ok ifølge side 19. Jeg er dog allerede låst til cc 60 på grunn av en tidligere konstruksjon, hvilket ifølge side 19 er for mye (bør være maks 2,15/4 = 53,75 cm). For å komme opp i cc 60 skal jeg altså ha 2,4 m mellom pilarene, hvilket krever 70x220 bjelker....
Men blar jeg litt ned til side 25; dimensjonering av gulvbjelker, så er min frie lengde altså 3,1 m hvilket for cc60 krever 45x120 C24. Ja, men da så, da er jeg trygg med mine cc60 tross alt? Eller?
De vil bare ha margin for å unngå at du belaster bjelkene for mye og får en ugunstig plassering langt fra et opplegg. Lenger fra et opplegg gir større moment på bjelken og mer eller større nedbøyning ved kritisk punkt som da blir mellom plintene. Derfor vil de trekke inn c/c på gulvbjelkene til avstand plint/4.
Du kan legge på c/c 600 da 537 mm ikke gir så mye i sammenhengen, du kan få en større nedbøyning enn normalt (les 5 mm ved maks belastning). De bør ha regnet med 50 kg eller 491 N/m2 i bundet last samt 2 kN/m2 (203 kg) i frilast og da kan du konstatere hvor mye du kommer til å belaste gulvet, og du vil aldri komme opp i 203 kg/m2 med møbler samt personer, så med andre ord kan du sove rolig. Bare ikke sett dit flygelet eller et 500 kg betongbord.
Siste kommentaren om side 25 handler ikke om bjelken i dette tilfellet, men bare om bjelkene. De antar at bjelken din tåler alt du belaster den med og tar kun utgangspunkt i gulvbjelkene. Grunnen til side 19 er at de tar hensyn til moment i bjelken samt at de vil få opplegg fra plintene.
Du kan legge på c/c 600 da 537 mm ikke gir så mye i sammenhengen, du kan få en større nedbøyning enn normalt (les 5 mm ved maks belastning). De bør ha regnet med 50 kg eller 491 N/m2 i bundet last samt 2 kN/m2 (203 kg) i frilast og da kan du konstatere hvor mye du kommer til å belaste gulvet, og du vil aldri komme opp i 203 kg/m2 med møbler samt personer, så med andre ord kan du sove rolig. Bare ikke sett dit flygelet eller et 500 kg betongbord.
Siste kommentaren om side 25 handler ikke om bjelken i dette tilfellet, men bare om bjelkene. De antar at bjelken din tåler alt du belaster den med og tar kun utgangspunkt i gulvbjelkene. Grunnen til side 19 er at de tar hensyn til moment i bjelken samt at de vil få opplegg fra plintene.
Ok, så D/4 sikter til å sikre at lasten alltid fordeles på et visst antall (4) punkter over bjelken.
Hvis vi tar eksemplet d=2,4m og cc600, har vi fire bjelker som belaster en bjelke mellom to plinter. Hvis jeg reduserer d til f.eks. 2m betyr det at bare tre bjelker havner innenfor d og dermed færre punkter som en gitt last fordeles på. Forstår jeg det riktig da?
Ligningen må vel henge sammen med dimensjonen på bjelken? Fordi momentet reduseres parallelt med d så tåler jo en gitt bjelke mer last med redusert d.
Altså: Fordi jeg er låst til cc60 bør jeg dimensjonere bjelken ut fra antagelsen d=2,4. Gitt at jeg ikke går ned i dimensjon på bjelken kan jeg da uten risiko redusere d (jo mer desto mer stabil konstruksjon).
Tenker jeg riktig? Jeg har ikke tenkt å sette et flygel på, men jeg kan ikke garantere at det aldri kommer til å bli satt ut et basseng, så jeg vil ikke jukse med konstruksjonen.
Forresten; Bonusspørsmål om bærekraft: Tommelfingerregelen sier at terrassebord skal være minst 22 mm tykke, men gjør ingen forskjell på for eksempel 28 eller 34. Jeg velger mellom 28x145 og 34x145 og forstår at den siste blir stivere, men det er ikke et fjell jeg konstruerer, så litt (praktisk talt umerkelig) svikt er ok. Men bør valget påvirke dimensjoneringen av bjelkene på noen måte?
Hvis vi tar eksemplet d=2,4m og cc600, har vi fire bjelker som belaster en bjelke mellom to plinter. Hvis jeg reduserer d til f.eks. 2m betyr det at bare tre bjelker havner innenfor d og dermed færre punkter som en gitt last fordeles på. Forstår jeg det riktig da?
Ligningen må vel henge sammen med dimensjonen på bjelken? Fordi momentet reduseres parallelt med d så tåler jo en gitt bjelke mer last med redusert d.
Altså: Fordi jeg er låst til cc60 bør jeg dimensjonere bjelken ut fra antagelsen d=2,4. Gitt at jeg ikke går ned i dimensjon på bjelken kan jeg da uten risiko redusere d (jo mer desto mer stabil konstruksjon).
Tenker jeg riktig? Jeg har ikke tenkt å sette et flygel på, men jeg kan ikke garantere at det aldri kommer til å bli satt ut et basseng, så jeg vil ikke jukse med konstruksjonen.
Forresten; Bonusspørsmål om bærekraft: Tommelfingerregelen sier at terrassebord skal være minst 22 mm tykke, men gjør ingen forskjell på for eksempel 28 eller 34. Jeg velger mellom 28x145 og 34x145 og forstår at den siste blir stivere, men det er ikke et fjell jeg konstruerer, så litt (praktisk talt umerkelig) svikt er ok. Men bør valget påvirke dimensjoneringen av bjelkene på noen måte?
Helt riktig at de vil fordele på 4 punkter i sin tabell over dim på bjelker, ellers blir deres tabell kjempe stor og får ikke plass i lommeformat.
Vil du ha 2,4 meter mellom plintene og oppfylle kravene for c/c 600mm må du gå opp på limtre eller annen type bjelke da de bare har med opp til 220 høye K24 bjelker i sin tabell.
Se side 20 for limtre bjelker, men du må grave dypere for samme høyde.
Når det gjelder bonusspørsmålet er det slik at man begynner dim fra der man har lasten dvs. gulvet, da tar man og kontrollerer tykkelse mot c/c på gulvbjelker og så mot bjelke og bjelke mot plintene og så plintene mot bakken. Har du lengre c/c enn 600 bør man øke til 28 eller 34.
Alt handler om nedbøyning som er akseptabel. Du vil ikke at gulvet skal helle 1 cm mellom bjelkene om man står midt imellom. Det får man om man har for langt mellom eller for lav konstruksjon på gulvet, prøv med en planke 22 mm, stå midt på den med opplegg c/c 400, 600, 800 og 1000 og du vil få ulik nedbøyning på midten. Det samme gjelder for bjelken bare at den tar opp last fra flere gulvbjelker og større flate av gulvet.
Håper jeg er tydelig, det er ikke lett uten å tegne noen ganger.
Vil du ha 2,4 meter mellom plintene og oppfylle kravene for c/c 600mm må du gå opp på limtre eller annen type bjelke da de bare har med opp til 220 høye K24 bjelker i sin tabell.
Se side 20 for limtre bjelker, men du må grave dypere for samme høyde.
Når det gjelder bonusspørsmålet er det slik at man begynner dim fra der man har lasten dvs. gulvet, da tar man og kontrollerer tykkelse mot c/c på gulvbjelker og så mot bjelke og bjelke mot plintene og så plintene mot bakken. Har du lengre c/c enn 600 bør man øke til 28 eller 34.
Alt handler om nedbøyning som er akseptabel. Du vil ikke at gulvet skal helle 1 cm mellom bjelkene om man står midt imellom. Det får man om man har for langt mellom eller for lav konstruksjon på gulvet, prøv med en planke 22 mm, stå midt på den med opplegg c/c 400, 600, 800 og 1000 og du vil få ulik nedbøyning på midten. Det samme gjelder for bjelken bare at den tar opp last fra flere gulvbjelker og større flate av gulvet.
Håper jeg er tydelig, det er ikke lett uten å tegne noen ganger.
Jeg funderte på dette et par runder til. Det går an å få 3 punkter om gulvlektene ligger akkurat på pilarne. Og siden den eneste grunnen jeg kan komme på til at cc mellom gulvlekter skal reduseres parallelt med avstanden mellom pilarne er for å unngå at lasten fordeles på for få punkter, burde likningen være i trinn/intervall snarere enn lineær.
Eksempel: d=2m -> cc 50 cm. Det verste for bjelken og en gitt last er da om gulvlektene ligger akkurat på pilaren, siden vi da bare har tre punkter som belaster bjelken. Hvis jeg nå reduserer d til 1,9....1,8....1,7...1,6... så endres ingenting bortsett fra at momentet mot pilarne reduseres (bjelkens bæreevne øker) siden det fortsatt ikke kan bli færre enn 3 gulvlekter mellom to pilarer. Ved d = 1,5 derimot oppstår situasjonen at det kan bli 2 punkter og den lokale kraften mot bjelken øker (gitt ugunstig plassering av last).
Altså burde retningslinjen være at cc skal være mellom d/4 og d/3, og mine cc 600 på d=2,15 er med andre ord helt i orden
Med forbehold om at jeg helt har misset poenget
Eksempel: d=2m -> cc 50 cm. Det verste for bjelken og en gitt last er da om gulvlektene ligger akkurat på pilaren, siden vi da bare har tre punkter som belaster bjelken. Hvis jeg nå reduserer d til 1,9....1,8....1,7...1,6... så endres ingenting bortsett fra at momentet mot pilarne reduseres (bjelkens bæreevne øker) siden det fortsatt ikke kan bli færre enn 3 gulvlekter mellom to pilarer. Ved d = 1,5 derimot oppstår situasjonen at det kan bli 2 punkter og den lokale kraften mot bjelken øker (gitt ugunstig plassering av last).
Altså burde retningslinjen være at cc skal være mellom d/4 og d/3, og mine cc 600 på d=2,15 er med andre ord helt i orden
Med forbehold om at jeg helt har misset poenget
Nei, ligger en last rett over søylen blir det ikke noe moment i bærelinjen for den i det hele tatt, dvs moment av 3 laster i stedet for 4 som du får ved innfestning når søylen er midt mellom 2 gulvbjelker.
Moment er en bevegelse og når du stopper bevegelsen får du en nedbøyning. Kraften fra gulvbjelkene skaper moment i bærelinjen. (se fig klarte ikke å la være å tegne)
Så de har D/4 for å være sikre at du skal klare deg.
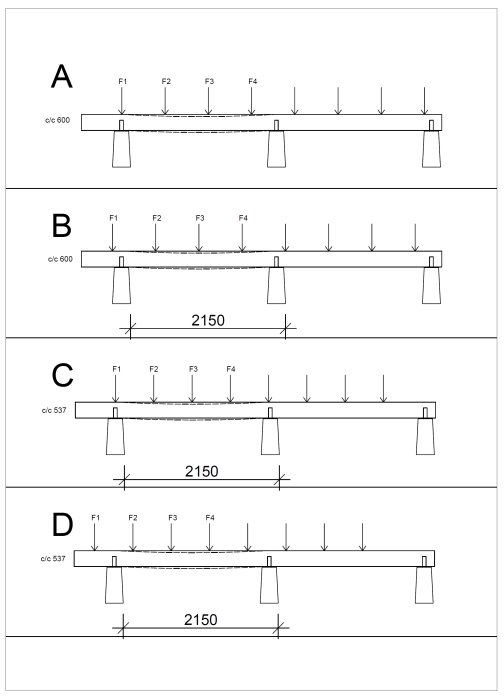
Kommentar til figur,
I A og B har jeg c/c 600 som du vil ha, A er rett over søyle og B er verste tilfelle man kan få med last midt mellom søyler dvs lengste avstanden til innfestning (blir største momentet eksponentielt da man tar kraft ganger avstand)
I C og D er c/c redusert til D/4 537 mm, dette gir da en lavere last per F1 - F4 sammenlignet med A og B. da hver gulvbjelke skal i A og B ta opp 0,6x1,55x2kN og i C og D 0,537x1,55x2kN
A og B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C og D for F1 - F4 = 1,66 + ,5kN = 2,16 kN
Forskjell 2,36-2,16 = 0,2kN eller ca. 10% mer i A og B.
Når du får verste tilfelle på begge havner du midt mellom innfestningene dvs 2,15/2 = 1,075 m gange dette med tidligere resultat og du får 2,53kNm for A og B samt 2,32 kNm for C og D.
Dvs C og D vil ha mindre moment enn A og B.
Til slutt kan jeg være enig i at de bruker et stumpet tall for å kalkulere riktig cc avstand, men å legge med en kurve for å lese av for å dele forskjellige d med 3,5 til 4,5 i en eksponentiell kurve hadde bare vært tungvint.
Moment er en bevegelse og når du stopper bevegelsen får du en nedbøyning. Kraften fra gulvbjelkene skaper moment i bærelinjen. (se fig klarte ikke å la være å tegne)
Så de har D/4 for å være sikre at du skal klare deg.
Kommentar til figur,
I A og B har jeg c/c 600 som du vil ha, A er rett over søyle og B er verste tilfelle man kan få med last midt mellom søyler dvs lengste avstanden til innfestning (blir største momentet eksponentielt da man tar kraft ganger avstand)
I C og D er c/c redusert til D/4 537 mm, dette gir da en lavere last per F1 - F4 sammenlignet med A og B. da hver gulvbjelke skal i A og B ta opp 0,6x1,55x2kN og i C og D 0,537x1,55x2kN
A og B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C og D for F1 - F4 = 1,66 + ,5kN = 2,16 kN
Forskjell 2,36-2,16 = 0,2kN eller ca. 10% mer i A og B.
Når du får verste tilfelle på begge havner du midt mellom innfestningene dvs 2,15/2 = 1,075 m gange dette med tidligere resultat og du får 2,53kNm for A og B samt 2,32 kNm for C og D.
Dvs C og D vil ha mindre moment enn A og B.
Til slutt kan jeg være enig i at de bruker et stumpet tall for å kalkulere riktig cc avstand, men å legge med en kurve for å lese av for å dele forskjellige d med 3,5 til 4,5 i en eksponentiell kurve hadde bare vært tungvint.
Klikk her for å svare