Hei kaikki,
olen jumissa yksinkertaisessa mekaniikkakysymyksessä, huokaus.
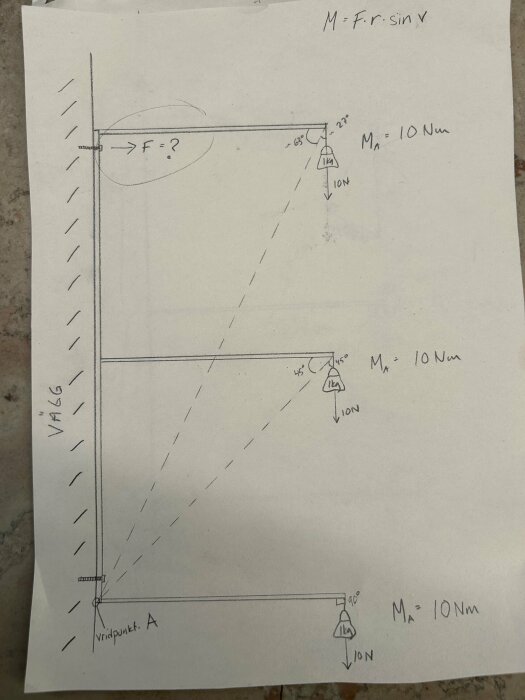
Yritän laskea voiman, joka vaikuttaa konsolin yläkiinnitykseen, jossa on kolme tasoa. Eli voiman, joka aikoo vetää ruuvin ulos seinästä, kun hyllytasot kuormitetaan.
Ajattelin laskea vääntömomentin vääntöpisteessä (alimman kohdalla konsolin osassa, joka on seinää vasten).
Ymmärrän, että on paljon muita voimia mukana, mutta olettakaa, että konsoli on niveltynyt siinä kohdassa. Ohita kuvan alempi ruuvi.
Minusta tuntuu, että kaikki tasot vaikuttavat samaan vääntömomenttiin, voiko se todella pitää paikkansa? Laskenko väärin?
Miten laskisitte voiman?
Ystävällisin terveisin
Johan
olen jumissa yksinkertaisessa mekaniikkakysymyksessä, huokaus.
Yritän laskea voiman, joka vaikuttaa konsolin yläkiinnitykseen, jossa on kolme tasoa. Eli voiman, joka aikoo vetää ruuvin ulos seinästä, kun hyllytasot kuormitetaan.
Ajattelin laskea vääntömomentin vääntöpisteessä (alimman kohdalla konsolin osassa, joka on seinää vasten).
Ymmärrän, että on paljon muita voimia mukana, mutta olettakaa, että konsoli on niveltynyt siinä kohdassa. Ohita kuvan alempi ruuvi.
Minusta tuntuu, että kaikki tasot vaikuttavat samaan vääntömomenttiin, voiko se todella pitää paikkansa? Laskenko väärin?
Miten laskisitte voiman?
Ystävällisin terveisin
Johan
Paras vastaus
Paholainen piilee yksityiskohdissa. Juuri tämä "yksinkertainen mekaniikkakysymys" voi joskus yksinkertaistaa ongelmaa enemmän kuin ajattelee. Jos hylly todella näyttää luonnokselta, takaseinä tulee olemaan taipuva. Näin ollen saatat kohdata suurempaa voimaa yläruuvissa, kun ylintä hyllylevyä kuormitetaan. Toisaalta, jos kyseessä on hylly jossa on sivut, se ei tule taipumaan merkittävästi. Olet pohtinut laskelman oikein. Ja niin kauan kuin hylly on kohtuullisen jäykkä ja kiinnitetty kunnolla, laskelma pätee myös käytännössä.
R RiKr sanoi:
Hei,A ArneTW sanoi:
Kiitos vastauksesta!
En ymmärrä, miten lasket, mutta haluaisin mielelläni ymmärtää, jos voisit selittää tarkemmin, näyttää?
Terveisin
Johan
käsittele jokaista hyllytasoa erikseen...Attefallshuset sanoi:
Oletan, että jokainen hyllytaso on 1m ja välimatka on myös 1m.
laske momentti pisteen A ympärillä.
Alin hyllytaso
1m * 10N = 2m x XN, X=5N
hyllytaso2
(1m+1m)*10N=2m*XN, X=10N
hyllytaso3
(1m+1m+1m)*10N=2m*XN, X=15N
lisää tulokseksi 30N.
Että hyllytasot ovat 90° ulospäin ei merkitse mitään... Voit yhtä hyvin ajatella, että ne seisovat suoraan ylöspäin.
ohitan kaiken oman painon jne sekä myös leikkausvoimat/kitkan ja kaikki on 100% jäykkää.
/ATW
Onhan siellä muitakin voimia... leikkausvoima eli voima pystysuunnassa alas seinää pitkin.T topmount sanoi:
30N jos kyseessä on yksi ruuvi, mutta jos lasketaan mukaan 2 ruuvia, arvo on välillä 0 ja 30N.
Sitten tulee mukaan kitka jne.
Voi tehdä asiasta monimutkaista...
Ymmärsin, että TS kysyi voiman komponenttia, joka haluaa repiä ruuvin seinästä...
/ATW
Onhan etäisyys painopisteestä ja kääntöpisteestä A mielenkiintoinen. Ja se on sama kaikille hyllytasolle. Mitä sinä lisäät? Väitä että kaikilla kolmella painolla on vaikutus 10 Nm A:n ympärillä aivan kuten @Attefallshuset on kirjoittanut luonnokseensa. Ja siten yhteensä 15 N vetovoima ruuvin suunnassa.A ArneTW sanoi:
Mielestäni olet väärässä... Hyllytasojen pystysuoralla sijainnilla on merkitystä mielestäni.A Avemo sanoi:
Eli jos lisäät hyllytason, joka sijaitsee 1000m korkeudella, saisit huomattavan lisäyksen eikä vain 5N lisää...
Saat 10Nm kunkin hyllytason kiinnityksessä, mutta et voi vain siirtää sitä alas A:han.
/ATW
TS:n teoreettisessa ja staattisessa mallissa, jossa "kääntökohta A" on nivelöity tuki, asia on näin.T topmount sanoi:
Todellisuudessa se on tietysti monimutkaisempaa, mutta jos on ajateltu oikein, malli kattaa sen, mikä on oleellista.
Harrastajasähköasentaja
· Värmland, Molkom
· 26 131 viestiä
Mikä oli vastaus, eli kuinka järkeillään päätyäkseen ratkaisuun?
Ensin lasketaan kuinka suuri vääntömomentti kukin hyllylevy tuottaa pisteessä A.
Vain se voiman komponentti, joka on kohtisuorassa vääntövarteen nähden, tuottaa vääntömomentin. Eli kun vedät jakoavaimella, vain se voima, joka kohdistuu "kiertosuuntaan", luo vääntömomentin.
Tämän perusteella voidaan helposti määrittää vääntömomentti, jonka alin hyllytaso tuottaa, koska tämä voima on kokonaisuudessaan kohtisuorassa vipuvartta (hyllyä) vastaan. Vääntömomentti = voima × vipuvarren pituus: τ = Fr.
TS:lla on voima 10 N ja hän päätyy ilmeisesti 10 Nm:iin, mikä tarkoittaa, että voimme päätellä hyllylevyn pituuden olevan 1 m.
Toisen hyllytason kohdalla TS ajattelee, että kulma selän ja hyllyn välillä muodostaa kuvitellun vipuvarren pisteestä A kohtaan, jossa voima kohdistuu. Voima ei kuitenkaan tässä kohdin kohdistu kohtisuoraan kuviteltua vipuvartta vastaan, ja TS:n on siksi laskettava se voiman komponentti, joka on kohtisuorassa vipuvartta vastaan, mikä on F⊥= |F| sin θ, missä F on voima ja θ on kulma vipuvartta vastaan. Tämä kulma on tässä tapauksessa 45°, joten F⊥ = 10 × sin 45° = 10 × √2 / 2 = 5 × √2.
Kulma 45° paljastaa myös, että matka toiseen hyllyyn on 1 m. Kuvitellun vipuvarren pituus saadaan Pythagoraan lauseella: c = √(a² + b²) = √(1² + 1²) = √2.
Nyt voimme laskea vääntömomentin, jonka toinen hyllytaso tuottaa: τ = Fr = 5 × √2 × √2 = 5 × √2² = 5 × 2 = 10 Nm.
Tarkkaavaiset huomaavat tässä voiman vektorin ja kuvitellun vipuvarren pituuden välisen yhteyden ja tajuavat, että etäisyys hyllyjen välillä voidaan eliminoida yhtälöstä. Kaikki hyllyt tuottavat saman vääntömomentin korkeudesta riippumatta.
Yhteismääräinen vääntömomentti voidaan siis helposti määrittää 3 × 1 × 10 = 30 Nm.
Jotta voimme sitten laskea voiman F, kun vääntömomentti on tiedossa, laskemme taaksepäin:
τ = Fr → 30 = F × 2 → F = 30 / 2 = 15 N.