3 254 lukukertaa ·
5 vastausta
3k lukukertaa
5 vastausta
Apua Svenskt Trän lehtimiehen tulkintaan
Olen laskemassa uutta terassia ja käytän tätä
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
Sivulla 19 sanotaan, että lattialankkujen etäisyyden keskipisteiden välillä tulisi olla enintään pilariväli/4. Tämä tarkoittaa siis, että jos asetan enemmän pilareita (vähennän pilariväliä), minun pitäisi myös asettaa lattialankut tiheämmin. Miksi näin? Tuntuu epäloogiselta minusta!
Minun tapauksessani olen ajatellut olevan 2,15 pilarien välillä vapaalla pituudella 3,1m ja 45x220 kantopuu. Ok sivun 19 mukaan. Olen kuitenkin jo sidottu cc 60:een aiemman rakenteen vuoksi, mikä sivun 19 mukaan on liikaa (pitäisi olla max 2,15/4 = 53,75 cm). Jotta pääsisin cc 60:een, minun on siis oltava 2,4 m pilarien välillä, mikä vaatii 70x220 lankkuja...
Mutta kun selaan hieman alas sivulle 25; lattialankkujen mitoitus, minun vapaa pituuteni on siis 3,1 m, mikä cc 60:lle vaatii 45x120 C24. No niin, sittenhän olen turvassa cc 60:lläni kaikesta huolimatta? Vai?
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
Sivulla 19 sanotaan, että lattialankkujen etäisyyden keskipisteiden välillä tulisi olla enintään pilariväli/4. Tämä tarkoittaa siis, että jos asetan enemmän pilareita (vähennän pilariväliä), minun pitäisi myös asettaa lattialankut tiheämmin. Miksi näin? Tuntuu epäloogiselta minusta!
Minun tapauksessani olen ajatellut olevan 2,15 pilarien välillä vapaalla pituudella 3,1m ja 45x220 kantopuu. Ok sivun 19 mukaan. Olen kuitenkin jo sidottu cc 60:een aiemman rakenteen vuoksi, mikä sivun 19 mukaan on liikaa (pitäisi olla max 2,15/4 = 53,75 cm). Jotta pääsisin cc 60:een, minun on siis oltava 2,4 m pilarien välillä, mikä vaatii 70x220 lankkuja...
Mutta kun selaan hieman alas sivulle 25; lattialankkujen mitoitus, minun vapaa pituuteni on siis 3,1 m, mikä cc 60:lle vaatii 45x120 C24. No niin, sittenhän olen turvassa cc 60:lläni kaikesta huolimatta? Vai?
He haluavat vain varmistaa, että et ylikuormita kantolevyjä liikaa ja saa epäedullista sijoitusta liian kaukana tukipisteestä. Pitkä etäisyys tukipisteestä aiheuttaa suuremman momentin kantolevyyn ja enemmän tai suurempaa taipumaa kriittisessä pisteessä, joka on silloin palkkien välissä. Siksi he haluavat vetää cc-etäisyyden lattian kannattimille etäisyyteen tuki/4.
Voit käyttää cc 600, koska 537 mm ei merkitse paljon tässä yhteydessä, voit saada suuremman taipuman kuin normaalisti (lue 5 mm maksimikuormituksessa). He ovat todennäköisesti laskeneet 50 kg tai 491N/m2 kiinteällä kuormalla sekä 2kN/m2 (203 kg) vapaalla kuormalla, ja voit todeta, kuinka paljon aiot kuormittaa lattiaa, etkä koskaan saavuta 203 kg/m2 huonekaluilla ja henkilöillä, joten voit toisin sanoen nukkua rauhassa. Älä vain laita sinne flyygeliä tai 500 kg betonipöytää.
Viimeinen kommentti sivusta 25 ei koske kantolevyä tässä tapauksessa, vaan ainoastaan palkkeja. He olettavat, että kantolevysi kestää kaiken, mitä siihen kuormitat, ja keskittyvät vain lattian kannattimiin. Syy sivulle 19 on se, että he ottavat huomioon momentin kantolevyssä sekä haluavat saada tukea palkkien välille.
Voit käyttää cc 600, koska 537 mm ei merkitse paljon tässä yhteydessä, voit saada suuremman taipuman kuin normaalisti (lue 5 mm maksimikuormituksessa). He ovat todennäköisesti laskeneet 50 kg tai 491N/m2 kiinteällä kuormalla sekä 2kN/m2 (203 kg) vapaalla kuormalla, ja voit todeta, kuinka paljon aiot kuormittaa lattiaa, etkä koskaan saavuta 203 kg/m2 huonekaluilla ja henkilöillä, joten voit toisin sanoen nukkua rauhassa. Älä vain laita sinne flyygeliä tai 500 kg betonipöytää.
Viimeinen kommentti sivusta 25 ei koske kantolevyä tässä tapauksessa, vaan ainoastaan palkkeja. He olettavat, että kantolevysi kestää kaiken, mitä siihen kuormitat, ja keskittyvät vain lattian kannattimiin. Syy sivulle 19 on se, että he ottavat huomioon momentin kantolevyssä sekä haluavat saada tukea palkkien välille.
Ok, joten D/4 tarkoittaa, että kuorma jaetaan aina tietylle määrälle (4) kohtia kantopalkin yli.
Jos otamme esimerkiksi d=2,4m ja cc600, meillä on neljä palkkia, jotka kuormittavat kantopalkkia kahden pilarin välillä. Jos pienennän d esimerkiksi 2 metriin, se tarkoittaa, että vain kolme palkkia mahtuvat d:n sisään ja näin ollen kuorma jakautuu harvemmille pisteille. Ymmärränkö oikein?
Yhtälön täytyy kuitenkin liittyä kantopalkin mittoihin? Koska momentti pienenee samansuuntaisesti d:n kanssa, kestää annettu kantopalkki enemmän kuormitusta pienemmällä d:llä.
Siis: Koska olen sidottu cc60:een, minun pitäisi mitoittaa kantopalkki olettaen d=2,4. Koska en aio pienentää kantopalkin mittoja, voin sitten ilman riskiä pienentää d:tä (mitä enemmän, sitä tukevampi rakenne).
Ajattelenko oikein? En aio asettaa flyygeliä sinne, mutta en voi taata, ettei koskaan aseteta uima-allasta, joten en halua fuskata rakenteen kanssa.
Muuten; Bonuskysymys kantavuudesta: Käsikirja sanoo, että terassin pitäisi olla vähintään 22 mm paksu, mutta ei tee eroa esimerkiksi 28 tai 34 välillä. Valitsen 28x145 ja 34x145 välillä ja ymmärrän, että jälkimmäinen on jäykempi, mutta en rakenna vuorta, joten pieni (periaatteessa huomaamaton) jousto on ok. Mutta pitäisikö valinnan vaikuttaa palkkien mitoitukseen jollain tavalla?
Jos otamme esimerkiksi d=2,4m ja cc600, meillä on neljä palkkia, jotka kuormittavat kantopalkkia kahden pilarin välillä. Jos pienennän d esimerkiksi 2 metriin, se tarkoittaa, että vain kolme palkkia mahtuvat d:n sisään ja näin ollen kuorma jakautuu harvemmille pisteille. Ymmärränkö oikein?
Yhtälön täytyy kuitenkin liittyä kantopalkin mittoihin? Koska momentti pienenee samansuuntaisesti d:n kanssa, kestää annettu kantopalkki enemmän kuormitusta pienemmällä d:llä.
Siis: Koska olen sidottu cc60:een, minun pitäisi mitoittaa kantopalkki olettaen d=2,4. Koska en aio pienentää kantopalkin mittoja, voin sitten ilman riskiä pienentää d:tä (mitä enemmän, sitä tukevampi rakenne).
Ajattelenko oikein? En aio asettaa flyygeliä sinne, mutta en voi taata, ettei koskaan aseteta uima-allasta, joten en halua fuskata rakenteen kanssa.
Muuten; Bonuskysymys kantavuudesta: Käsikirja sanoo, että terassin pitäisi olla vähintään 22 mm paksu, mutta ei tee eroa esimerkiksi 28 tai 34 välillä. Valitsen 28x145 ja 34x145 välillä ja ymmärrän, että jälkimmäinen on jäykempi, mutta en rakenna vuorta, joten pieni (periaatteessa huomaamaton) jousto on ok. Mutta pitäisikö valinnan vaikuttaa palkkien mitoitukseen jollain tavalla?
Täysin oikein, että he haluavat jakaa neljään kohtaan taulukossaan kantavien palkkien mitat, muuten heidän taulukkonsa kasvaa liian suureksi eikä mahdu taskukokoiseksi.
Jos haluat 2,4 metriä pilarien väliin ja täyttää vaatimukset c/c 600mm, on siirryttävä liimapuuhun tai muun tyyppiseen palkkiin, koska heidän taulukossaan on enintään 220 korkeita K24 kantavia palkkeja.
Katso sivu 20 liimapuu palkkeja varten, mutta joudut kaivamaan syvemmälle samaa korkeutta varten.
Bonuskysymyksestä on niin, että mitat aloitetaan siitä, missä on kuorma eli lattiasta, silloin tarkistetaan paksuus golvbjälkarin c/c-mittaa vastaan ja sitten kantavia palkkeja vastaan, ja kantavien palkkien kohdalla perustusta vastaan ja sitten perustusta maata vastaan. Jos sinulla on pidempi c/c kuin 600, kannattaa lisätä 28 tai 34.
Kyse on hyväksyttävästä taipumasta. Et halua, että lattia kallistuu 1 cm koolinkien välissä, jos seisot keskellä. Tämä tapahtuu, jos väli on liian pitkä tai lattian rakenne on liian matala. Kokeile 22 mm laudalla, seiso sen keskellä tuella c/c 400, 600, 800 ja 1000, ja huomaat erilaisen taipuman keskellä. Sama koskee kantavia palkkeja, vain että ne ottavat kuorman useammista golvbjälkereiltä ja suuremmalta lattiapinnalta.
Toivottavasti olen selkeä, joskus on vaikea selittää ilman piirtämistä.
Jos haluat 2,4 metriä pilarien väliin ja täyttää vaatimukset c/c 600mm, on siirryttävä liimapuuhun tai muun tyyppiseen palkkiin, koska heidän taulukossaan on enintään 220 korkeita K24 kantavia palkkeja.
Katso sivu 20 liimapuu palkkeja varten, mutta joudut kaivamaan syvemmälle samaa korkeutta varten.
Bonuskysymyksestä on niin, että mitat aloitetaan siitä, missä on kuorma eli lattiasta, silloin tarkistetaan paksuus golvbjälkarin c/c-mittaa vastaan ja sitten kantavia palkkeja vastaan, ja kantavien palkkien kohdalla perustusta vastaan ja sitten perustusta maata vastaan. Jos sinulla on pidempi c/c kuin 600, kannattaa lisätä 28 tai 34.
Kyse on hyväksyttävästä taipumasta. Et halua, että lattia kallistuu 1 cm koolinkien välissä, jos seisot keskellä. Tämä tapahtuu, jos väli on liian pitkä tai lattian rakenne on liian matala. Kokeile 22 mm laudalla, seiso sen keskellä tuella c/c 400, 600, 800 ja 1000, ja huomaat erilaisen taipuman keskellä. Sama koskee kantavia palkkeja, vain että ne ottavat kuorman useammista golvbjälkereiltä ja suuremmalta lattiapinnalta.
Toivottavasti olen selkeä, joskus on vaikea selittää ilman piirtämistä.
Mietin tätä pari kertaa uudelleen. On mahdollista saada 3 pistettä, jos lattian tukipuut ovat suoraan pilareilla. Ja koska ainoa syy, jonka keksin siihen, miksi keskietäisyys lattian tukipuiden välillä pitäisi pienentyä samalla kun etäisyys pilarien välillä pienenee, on välttää kuorman jakautumista liian harvoille pisteille, yhtälön tulisi olla askel/väli-tyyppinen ennemmin kuin lineaarinen.
Esimerkki: d=2m -> cc 50 cm. Se huonoin mahdollinen tilanne kantoparrulle ja annetulle kuormalle on silloin, jos lattian tukipuut ovat suoraan pilarin päällä, koska silloin kuormitetaan kantoparrua vain kolmella pisteellä. Jos nyt pienennän d-arvon 1,9....1,8....1,7...1,6... niin mikään ei muutu paitsi momentti pilareita vastaan vähenee (kantoparrun kantokyky kasvaa), koska ei vieläkään voi olla vähemmän kuin 3 lattian tukipuuta kahden pilarin välillä. Kun d = 1,5 kuitenkin tilanne on, että voi olla 2 pistettä ja paikallinen voima kantoparrua vastaan kasvaa (olettaen epäsuotuisa kuorman sijoittelu).
Siis ohjeistuksen pitäisi olla, että cc on välillä d/4 ja d/3, ja minun cc 600, kun d=2,15, ovat toisin sanoen täysin ok
Varauksella, että olen kokonaan missannut pointin
Esimerkki: d=2m -> cc 50 cm. Se huonoin mahdollinen tilanne kantoparrulle ja annetulle kuormalle on silloin, jos lattian tukipuut ovat suoraan pilarin päällä, koska silloin kuormitetaan kantoparrua vain kolmella pisteellä. Jos nyt pienennän d-arvon 1,9....1,8....1,7...1,6... niin mikään ei muutu paitsi momentti pilareita vastaan vähenee (kantoparrun kantokyky kasvaa), koska ei vieläkään voi olla vähemmän kuin 3 lattian tukipuuta kahden pilarin välillä. Kun d = 1,5 kuitenkin tilanne on, että voi olla 2 pistettä ja paikallinen voima kantoparrua vastaan kasvaa (olettaen epäsuotuisa kuorman sijoittelu).
Siis ohjeistuksen pitäisi olla, että cc on välillä d/4 ja d/3, ja minun cc 600, kun d=2,15, ovat toisin sanoen täysin ok
Varauksella, että olen kokonaan missannut pointin
Ei, jos kuorma on suoraan plintin yläpuolella, siitä ei synny momenttia kantavaan palkkiin, eli kolme kuormaa neljän sijasta, joka syntyy, kun plintti on kahden lattianiskapuun välissä.
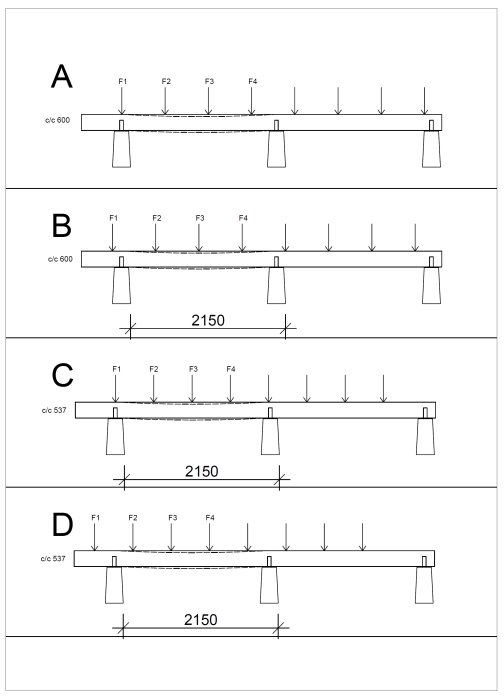
Momentti on liike, ja kun pysäytät liikkeen, saat taipuman. Lattianiskapuiden voima luo momentin kantavaan palkkiin. (katso kuva, en voinut vastustaa piirtämistä)
Siksi he ovat käyttäneet D/4 varmistaakseen, että se kestää.
Kommentti kuvaan,
Kohdissa A ja B on c/c 600, kuten haluat, A on suoraan plintin päällä ja B on pahimmassa mahdollisessa tilanteessa, kun kuorma on plinttien välissä eli suurin etäisyys tukeen (momentti kasvaa eksponentiaalisesti, kun voima kerrotaan etäisyydellä).
Kohdissa C ja D c/c on pienennetty D/4 537 mm, mikä antaa alhaisemman kuorman per F1 - F4 verrattuna A:n ja B:n. Jokaisen lattianiskapuun pitää A:ssa ja B:ssä kantaa 0,6x1,55x2kN ja C:ssä ja D:ssä 0,537x1,55x2kN.
A ja B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C ja D F1 - F4 = 1,66 + ,5kN = 2,16 kN
Ero 2,36-2,16 = 0,2kN eli noin 10 % enemmän A:lla ja B:llä.
Kun sinulla on pahin tilanne molemmissa, päädyt tukien puoliväliin eli 2,15/2 = 1,075 m, kerro tämä aikaisemmalla tuloksella ja saat 2,53 kNm A:lle ja B:lle sekä 2,32 kNm C:lle ja D:lle.
Eli C:llä ja D:llä tulee olemaan vähemmän momenttia kuin A:lla ja B:llä.
Lopuksi voin olla samaa mieltä siitä, että he käyttävät karkeaa lukua oikean cc-etäisyyden laskemiseksi, mutta kurvin lisääminen eri d:n jakamiseksi 3,5:stä 4,5:een eksponentiaalisessa kurvissa olisi ollut vain hankalaa.
Momentti on liike, ja kun pysäytät liikkeen, saat taipuman. Lattianiskapuiden voima luo momentin kantavaan palkkiin. (katso kuva, en voinut vastustaa piirtämistä)
Siksi he ovat käyttäneet D/4 varmistaakseen, että se kestää.
Kommentti kuvaan,
Kohdissa A ja B on c/c 600, kuten haluat, A on suoraan plintin päällä ja B on pahimmassa mahdollisessa tilanteessa, kun kuorma on plinttien välissä eli suurin etäisyys tukeen (momentti kasvaa eksponentiaalisesti, kun voima kerrotaan etäisyydellä).
Kohdissa C ja D c/c on pienennetty D/4 537 mm, mikä antaa alhaisemman kuorman per F1 - F4 verrattuna A:n ja B:n. Jokaisen lattianiskapuun pitää A:ssa ja B:ssä kantaa 0,6x1,55x2kN ja C:ssä ja D:ssä 0,537x1,55x2kN.
A ja B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C ja D F1 - F4 = 1,66 + ,5kN = 2,16 kN
Ero 2,36-2,16 = 0,2kN eli noin 10 % enemmän A:lla ja B:llä.
Kun sinulla on pahin tilanne molemmissa, päädyt tukien puoliväliin eli 2,15/2 = 1,075 m, kerro tämä aikaisemmalla tuloksella ja saat 2,53 kNm A:lle ja B:lle sekä 2,32 kNm C:lle ja D:lle.
Eli C:llä ja D:llä tulee olemaan vähemmän momenttia kuin A:lla ja B:llä.
Lopuksi voin olla samaa mieltä siitä, että he käyttävät karkeaa lukua oikean cc-etäisyyden laskemiseksi, mutta kurvin lisääminen eri d:n jakamiseksi 3,5:stä 4,5:een eksponentiaalisessa kurvissa olisi ollut vain hankalaa.
Klikkaa tästä vastataksesi