20,355 views ·
38 replies
20k views
38 replies
Calculate U-value for construction
A Anton Svensk said:Glad it's appreciated!
I can bring out a figure showing the inside tonight.
What do you think about a comparison of different solutions resulting in the same wall thickness?
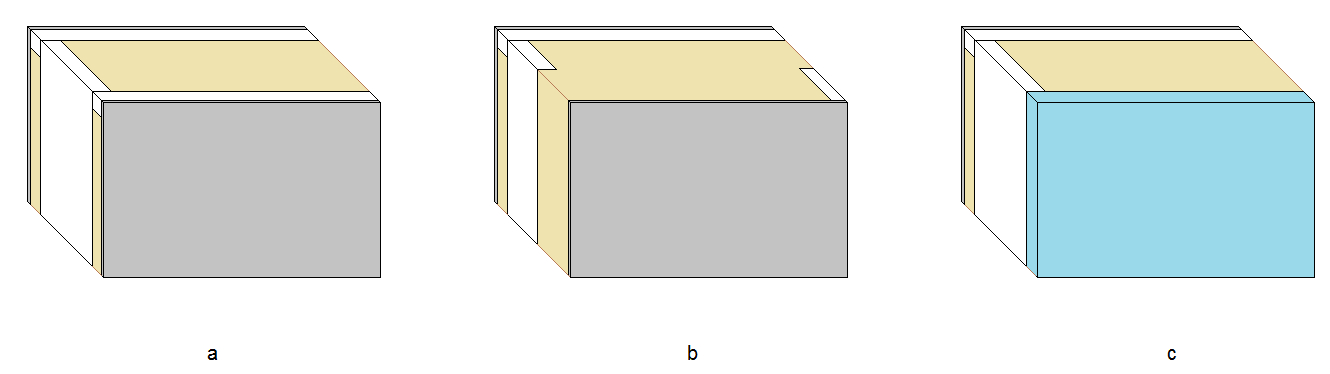
a. Exterior gypsum + 45 insulation (horizontal) + 145 insulation (vertical) + 45 insulated installation layer + gypsum
b. Exterior gypsum + 95 insulation (vertical) + 95 insulation (vertical) + 45 insulated installation layer + gypsum
c. STEICOuniversal (52 mm) + 145 insulation (vertical) + 45 insulated installation layer + gypsum
[bild]
Any other solution that is interesting? Light beam (like masonitebeam, swelite-beam, hunton light beam)?
/Anton
I tried running these options. Result:
a: U = 0.171
b: U = 0.170
c: U = 0.174
In summary, these solutions are practically identical when it comes to U-value. Surprisingly little difference, I must say.
/Anton
Know-It-All
· Västra Götaland
· 11 967 posts
I find this super interesting!
The part about how much energy can be saved through a "thermal mass" wall is very unexplored/presented. The U-value of the wall dictates how much energy leaks out, but the heating system doesn't have to work as hard during cold snaps.
It would be interesting to see a comparison between different wall types in various thicknesses. Like the reduced importance of thermal bridges with thicker walls. Does this calculation model take a stance on thermal radiation, does reflective foil make a difference?
The part about how much energy can be saved through a "thermal mass" wall is very unexplored/presented. The U-value of the wall dictates how much energy leaks out, but the heating system doesn't have to work as hard during cold snaps.
It would be interesting to see a comparison between different wall types in various thicknesses. Like the reduced importance of thermal bridges with thicker walls. Does this calculation model take a stance on thermal radiation, does reflective foil make a difference?
Several years ago, in connection with a project that fortunately never materialized, I read an English manual on tropical construction that was a real eye-opener. The manual contained several curves of the same type that TS has shown. They were likely the results of practical lab experiments.
If one wants to develop a comprehensive model for external wall constructions, one should of course also take into account the inward heat radiation, which argues for a material with high heat capacity closest to the room.
If one wants to develop a comprehensive model for external wall constructions, one should of course also take into account the inward heat radiation, which argues for a material with high heat capacity closest to the room.
FunJohannes Carlsson said:
I find this extremely interesting!
The aspect of how much energy can be saved through a "thermal mass" wall is very underexplored/presented. The U-value of the wall controls how much energy leaks out, but the heating system doesn't have to work as hard during cold snaps.
It would be interesting to see a comparison between different wall types in various thicknesses. Like the reduced significance of thermal bridges with thicker walls.
Does this calculation model consider radiant heat, does reflective foil make a difference?
I agree that the information is lacking. I have found some brands that talk about thermal mass (cellulose and wood fiber insulation manufacturers) and some, as mentioned, present values for Phase shift (STEICO and GUTEX). That's about it. They also talk about reduced total energy consumption if the temperature outside drops to low levels at night but is high during the day (spring and autumn). You then get a wall that is heated during the day by solar radiation and higher ambient temperature and doesn't have time to cool down at night.
The model doesn't take radiant heat into account as it stands now. It can probably be included, even though I haven't tried. Where were you thinking the foil should be placed?
/Anton
Interesting!J justusandersson said:Several years ago, in connection with a project that fortunately never materialized, I read an English handbook on tropical construction that was a real eye-opener. The handbook contained several curves of the same type as those TS has shown. They were probably the results of practical lab tests.
If one wants to develop a total model for exterior wall constructions, one should of course also consider heat radiation inward, which argues for a material with high heat capacity closest to the room.
How do you think the heat radiation into the room affects it? Shouldn't the temperature of the different surfaces in the room be nearly identical? I can imagine that radiation should be included in the equation when we look at the facade, which is why I chose not to include the facade material but calculate from the air gap inward.
/Anton
Know-It-All
· Västra Götaland
· 11 967 posts
I have seen some who advocate for a metal foil behind the drywall to reduce heat radiation outwards, but the question is how much is already stopped by the drywall.
I have also seen plates intended to be mounted on the wall behind a radiator, but I'm unsure about the effectiveness; you can't really trust the selling companies directly.
Could possibly be on the outside in warm countries (metal facade?)
If one could calculate the autumn/spring temperature and figure out how much is involved, it would be interesting. After all, it's the total energy consumption over the year that is most important.
I have also seen plates intended to be mounted on the wall behind a radiator, but I'm unsure about the effectiveness; you can't really trust the selling companies directly.
Could possibly be on the outside in warm countries (metal facade?)
If one could calculate the autumn/spring temperature and figure out how much is involved, it would be interesting. After all, it's the total energy consumption over the year that is most important.
Phase shift for cases a, b, and c above
I ran the model for phase shift for the three geometries in post #16.
a: dt = 3.6 h
b: dt = 4 h
c: dt = 6.4 h
In all these calculations, I used mineral wool as insulation. If I switch to wood fiber insulation (STEICO flex), the results are instead:
a: dt = 7.4 h
b: dt = 7.5 h
c: dt = 9.2 h
In addition to the phase shift, manufacturers also talk about an amplitude factor, meaning how much the amplitude of the outdoor temperature fluctuation is damped. They calculate it as (change in outdoor temperature)/(change in indoor temperature). Since I don't include indoor air in the model, I use (change in outdoor temperature)/(change in inner wall surface temperature). The fluctuations have an amplitude factor of (mineral wool/wood fiber insulation):
a: dt = 140/180
b: dt = 136/180
c: dt = 170/215
An amplitude factor of 215 means that if the outdoor temperature fluctuates by 20 °C, the temperature on the inner wall surface fluctuates by 0.092 °C (assuming the heating system keeps the air temperature at 20 °C and that only natural convection exists in the room, so no fan or such).
Here I compared the temperature on the inner wall surface for geometry a (mineral wool) with geometry c (wood fiber insulation):

From the figure, you can see that a has a lower U-value (higher temperature at t=0), but faster response and larger temperature fluctuations.
I'm a bit unsure how they modeled the room to derive a temperature that applies there. It becomes very dependent on how large it is and which materials are present. A room with a concrete floor, for example, takes much longer to heat up than if it has a wooden joist floor.
/Anton
I ran the model for phase shift for the three geometries in post #16.
a: dt = 3.6 h
b: dt = 4 h
c: dt = 6.4 h
In all these calculations, I used mineral wool as insulation. If I switch to wood fiber insulation (STEICO flex), the results are instead:
a: dt = 7.4 h
b: dt = 7.5 h
c: dt = 9.2 h
In addition to the phase shift, manufacturers also talk about an amplitude factor, meaning how much the amplitude of the outdoor temperature fluctuation is damped. They calculate it as (change in outdoor temperature)/(change in indoor temperature). Since I don't include indoor air in the model, I use (change in outdoor temperature)/(change in inner wall surface temperature). The fluctuations have an amplitude factor of (mineral wool/wood fiber insulation):
a: dt = 140/180
b: dt = 136/180
c: dt = 170/215
An amplitude factor of 215 means that if the outdoor temperature fluctuates by 20 °C, the temperature on the inner wall surface fluctuates by 0.092 °C (assuming the heating system keeps the air temperature at 20 °C and that only natural convection exists in the room, so no fan or such).
Here I compared the temperature on the inner wall surface for geometry a (mineral wool) with geometry c (wood fiber insulation):

From the figure, you can see that a has a lower U-value (higher temperature at t=0), but faster response and larger temperature fluctuations.
I'm a bit unsure how they modeled the room to derive a temperature that applies there. It becomes very dependent on how large it is and which materials are present. A room with a concrete floor, for example, takes much longer to heat up than if it has a wooden joist floor.
/Anton
Know-It-All
· Västra Götaland
· 11 967 posts
There is quite good temperature measurement data at SMHI (e.g. Landvetter Airport) where you can see temperature differences every day over many years. Available for download to Excel, maybe it's possible to create a realistic temperature difference curve to get more accurate values?
Absolutely, good idea! A simulation of a week, or maybe a whole season would be interesting. Then one should be able to see differences between constructions.Johannes Carlsson said:
/Anton
Do you take into account that the wall radiates heat to the room when the wall is warmer than the room (and vice versa)? It could at least on the smallest margin even out the conditions a bit...
Edit: Just noticed that you assume constant indoor temperature. The next step would be to include the inertia of the heating system to see how the indoor temperature varies?
Edit: Just noticed that you assume constant indoor temperature. The next step would be to include the inertia of the heating system to see how the indoor temperature varies?
I don't, as you've discovered. To include the inertia of the heating system, I need to assume a house that the wall belongs to. I'm a bit unsure how to choose that best... It might be possible to simplify the building to a "thermal point" with a specific thermal mass and then a transfer coefficient to transfer heat to and from the wall. Then you can set a heat source that tries to maintain the temperature at the thermal point at a chosen value (20 °C).useless said:
Do you take into account that the wall radiates heat to the room when the wall is warmer than the room (and vice versa)? That could at least on the smallest margin even out the conditions a bit...
Edit: I see now that you're considering constant indoor temperature. The next step will be to include the inertia of the heating system to see how the indoor temperature varies?
But regarding radiation, I think, as mentioned, that the effect is marginal as the temperatures between the surfaces should be so similar. As you can see in the curves in the previous post, the temperature on the wall's surface varies by less than ½ degree, even though the outdoor temperature varies by 20 °C.
I am now running a model where I have imported a year's worth of temperatures for Uppsala, with one data point per hour. The runtime seems to be about 30 minutes for such a model, compared to a few seconds for the previous models.
/Anton

