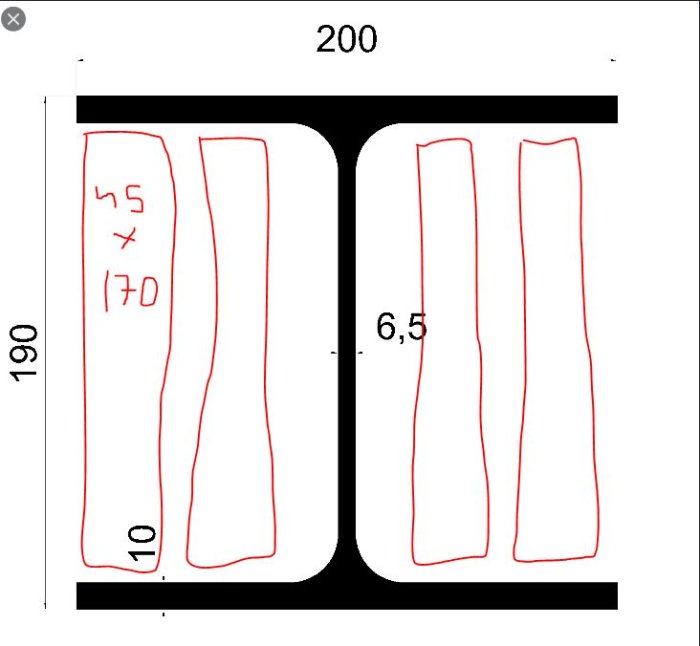
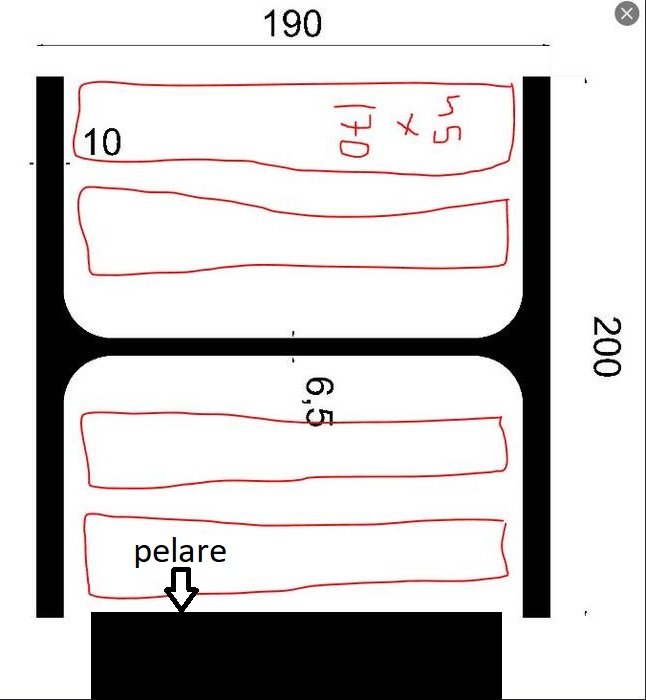
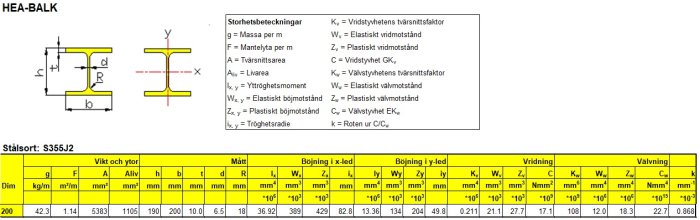
Fyldning med træ giver stort set ingenting i stivhed. Ved samme deformation vil stort set al last blive optaget af stålbjælken, som materialemæssigt har ca. 40 gange større stivhed end træ. Som tankeeksperiment: læg en elastik på en stållineal og udsæt sandwichen for trækbelastning. Hvilket materiale tager hovedparten af lasten?
Hvis du overhovedet skal få nogen hjælp af træreglerne, så skal de samarbejde med stålbjælken, dvs være "koblet" til hinanden og ikke bare "indkilet". Nu er der meget stor forskel mellem styrkerne af stål og træ, så den eventuelle tilføjelse her er nok at betragte som ubetydelig.
Hvordan mener du med koblede?R roli sagde:
tja man kan jo lege med tanken, at det bliver stivere, MEN når bjælken brister, er det en sådan kraft, at det ikke spiller nogen rolle, hvad dimensionen er, eller hvor mange brædder der er imellem ... MEN det er nu spekuleret i værste tænkelige scenario, at det klippes af på én gang ^^
men min teori i min lille lyserøde verden er, at man må beregne holdfastheden separat for bjælken (HEA fra størrelsen) og træet (C16 C24 C30), og så er spændvidde og belastning også noget, der vil være med og lege ... så kan man være nidkær med fastgørelsen af træværket... anvendelsen af boltpistol, hvor meget påvirker hullerne i bjælken osv.
der er meget
men min teori i min lille lyserøde verden er, at man må beregne holdfastheden separat for bjælken (HEA fra størrelsen) og træet (C16 C24 C30), og så er spændvidde og belastning også noget, der vil være med og lege ... så kan man være nidkær med fastgørelsen af træværket... anvendelsen af boltpistol, hvor meget påvirker hullerne i bjælken osv.
der er meget
Nej. I tænker forkert. Fastgørelsen af materialerne i hinanden har en ubetydelig betydning i dette tilfælde. Hvis det var en sandwichkonstruktion, ville det være vigtigt, men det er det ikke.
Nedbøjningen for en given geometri er direkte proportional med materialets E-modul. E-modulet er en materialkonstant for et materiales stivhed. Stål har ca. 210 GPa og træ et sted omkring 5 GPa. Det er en forskel på en faktor 40. Nu har de forskellige materialer ganske vist forskellige geometriske former, men det har lille betydning for ræsonnementet. Hvis vi sætter træ sammen med stål ifølge den første skitse, vil belastningen give den samme deformation, ikke sandt? De sidder jo sammen. Spændingen i en belastet konstruktion med en given deformation er direkte afhængig af E-modulet. Dette kaldes Hookes lov. Det fører til, at spændingen i stålet bliver så meget højere, at det stort set tager hele belastningen, og træet tager næsten ingen belastning overhovedet. Med så lav spænding i træet vil stivheden i den samlede konstruktion næsten ikke blive påvirket af, at man indsætter træ.
Nedbøjningen for en given geometri er direkte proportional med materialets E-modul. E-modulet er en materialkonstant for et materiales stivhed. Stål har ca. 210 GPa og træ et sted omkring 5 GPa. Det er en forskel på en faktor 40. Nu har de forskellige materialer ganske vist forskellige geometriske former, men det har lille betydning for ræsonnementet. Hvis vi sætter træ sammen med stål ifølge den første skitse, vil belastningen give den samme deformation, ikke sandt? De sidder jo sammen. Spændingen i en belastet konstruktion med en given deformation er direkte afhængig af E-modulet. Dette kaldes Hookes lov. Det fører til, at spændingen i stålet bliver så meget højere, at det stort set tager hele belastningen, og træet tager næsten ingen belastning overhovedet. Med så lav spænding i træet vil stivheden i den samlede konstruktion næsten ikke blive påvirket af, at man indsætter træ.
Senest redigeret:
Klik her for at svare