Jeg er ved at beregne en ny terrasse og bruger denne
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
På side 19 står der, at gulvbjælkerne skal have et centerafstand, der højest er plintafstand/4. Det betyder altså, at hvis jeg sætter flere plinter (reducerer plintafstanden), skal jeg også placere gulvbjælkerne tættere. Hvorfor det? Det føles ulogisk, synes jeg!
I mit tilfælde har jeg planlagt at have 2,15 mellem plinter på fri længde 3,1m og 45x220 bærende bjælke. Ok ifølge side 19. Jeg er dog allerede låst til cc 60 pga en tidligere konstruktion, hvilket ifølge side 19 er for meget (bør være max 2,15/4 = 53,75cm). For at komme op i cc 60 skal jeg altså have 2,4m mellem plinterne, hvilket kræver 70x220 reglar....
Men hvis jeg scroller lidt ned til side 25; dimensionering af gulvbjælker, så er min frie længde altså 3,1 m, hvilket for cc60 kræver 45x120 C24. Ja, men så er jeg sikker med mine cc60 trods alt? Eller?
https://www.svenskttra.se/siteassets/6-om-oss/publikationer/pdfer/lathund.pdf
På side 19 står der, at gulvbjælkerne skal have et centerafstand, der højest er plintafstand/4. Det betyder altså, at hvis jeg sætter flere plinter (reducerer plintafstanden), skal jeg også placere gulvbjælkerne tættere. Hvorfor det? Det føles ulogisk, synes jeg!
I mit tilfælde har jeg planlagt at have 2,15 mellem plinter på fri længde 3,1m og 45x220 bærende bjælke. Ok ifølge side 19. Jeg er dog allerede låst til cc 60 pga en tidligere konstruktion, hvilket ifølge side 19 er for meget (bør være max 2,15/4 = 53,75cm). For at komme op i cc 60 skal jeg altså have 2,4m mellem plinterne, hvilket kræver 70x220 reglar....
Men hvis jeg scroller lidt ned til side 25; dimensionering af gulvbjælker, så er min frie længde altså 3,1 m, hvilket for cc60 kræver 45x120 C24. Ja, men så er jeg sikker med mine cc60 trods alt? Eller?
De vil bare have margen for, at du ikke skal belaste bærbjælkerne for meget og få en ugunstig placering for langt væk fra et støttepunkt. Længere væk fra et støttepunkt giver større moment på bærbjælken og mere eller større nedbøjning ved kritisk punkt, som så bliver midt mellem stolperne. Derfor vil de trække c/c på gulvbjælkerne til afstand stolpe/4.
Du kan lægge på c/c 600, da 537 mm ikke giver så meget i sammenhængen, du kan få en større nedbøjning end normalt (læs 5 mm ved max belastning). De bør have regnet med 50kg eller 491N/m2 i fast last samt 2kN/m2 (203kg) i fri last, og da kan du konstatere, hvor meget du kommer til at belaste gulvet, og du kommer aldrig op i 203 kg/m2 møbler samt personer, så du kan med andre ord sove roligt. Stil ikke flyglet eller et 500kg betonbord der.
Sidste kommentar om side 25 handler ikke om bærbjælken i dette tilfælde, men kun om bjælkerne. De antager, at din bærbjælke klarer alt, du belaster den med, og antager kun ud fra gulvbjælkerne. Årsagen til side 19 er, at de tager hensyn til moment i bærbjælken samt at de vil få støtte fra stolperne.
Du kan lægge på c/c 600, da 537 mm ikke giver så meget i sammenhængen, du kan få en større nedbøjning end normalt (læs 5 mm ved max belastning). De bør have regnet med 50kg eller 491N/m2 i fast last samt 2kN/m2 (203kg) i fri last, og da kan du konstatere, hvor meget du kommer til at belaste gulvet, og du kommer aldrig op i 203 kg/m2 møbler samt personer, så du kan med andre ord sove roligt. Stil ikke flyglet eller et 500kg betonbord der.
Sidste kommentar om side 25 handler ikke om bærbjælken i dette tilfælde, men kun om bjælkerne. De antager, at din bærbjælke klarer alt, du belaster den med, og antager kun ud fra gulvbjælkerne. Årsagen til side 19 er, at de tager hensyn til moment i bærbjælken samt at de vil få støtte fra stolperne.
Ok, så D/4 sigter mod at sikre, at lasten altid fordeles på et vist antal (4) punkter over bæringen.
Hvis vi tager eksemplet d=2,4m og cc600, har vi fire regler, der belaster en bærende bjælke mellem to stolper. Hvis jeg reducerer d til f.eks. 2m, betyder det, at kun tre regler falder inden for d og således færre punkter, som en given last fordeles på. Forstår jeg det rigtigt?
Ligningen skal dog hænge sammen med dimensionen på bæringen, ikke? Fordi momentet reduceres parallelt med d, så tåler en given bærende bjælke mere last med reduceret d.
Altså: Da jeg er låst ved cc60, bør jeg dimensionere bæringen ud fra antagelsen d=2,4. Givet at jeg ikke reducerer dimensionen på den bærende bjælke, kan jeg da uden risiko reducere d (jo mere desto mere stabil konstruktion).
Tænker jeg rigtigt? Jeg har ikke tænkt mig at placere et flygel på, men jeg kan ikke garantere, at der aldrig vil blive stillet en pool op, så jeg vil ikke snyde med konstruktionen.
Forresten; Bonusspørgsmål om bæreevne: Lathunden siger, at trallen skal være mindst 22mm tyk, men gør ingen forskel på f.eks. 28 eller 34. Jeg vælger mellem 28x145 og 34x145 og forstår, at sidstnævnte bliver stivere, men det er ikke et bjerg, jeg konstruerer, så lidt (principielt umærkelig) svaj er ok. Men bør valget påvirke dimensioneringen af regler på nogen måde?
Hvis vi tager eksemplet d=2,4m og cc600, har vi fire regler, der belaster en bærende bjælke mellem to stolper. Hvis jeg reducerer d til f.eks. 2m, betyder det, at kun tre regler falder inden for d og således færre punkter, som en given last fordeles på. Forstår jeg det rigtigt?
Ligningen skal dog hænge sammen med dimensionen på bæringen, ikke? Fordi momentet reduceres parallelt med d, så tåler en given bærende bjælke mere last med reduceret d.
Altså: Da jeg er låst ved cc60, bør jeg dimensionere bæringen ud fra antagelsen d=2,4. Givet at jeg ikke reducerer dimensionen på den bærende bjælke, kan jeg da uden risiko reducere d (jo mere desto mere stabil konstruktion).
Tænker jeg rigtigt? Jeg har ikke tænkt mig at placere et flygel på, men jeg kan ikke garantere, at der aldrig vil blive stillet en pool op, så jeg vil ikke snyde med konstruktionen.
Forresten; Bonusspørgsmål om bæreevne: Lathunden siger, at trallen skal være mindst 22mm tyk, men gør ingen forskel på f.eks. 28 eller 34. Jeg vælger mellem 28x145 og 34x145 og forstår, at sidstnævnte bliver stivere, men det er ikke et bjerg, jeg konstruerer, så lidt (principielt umærkelig) svaj er ok. Men bør valget påvirke dimensioneringen af regler på nogen måde?
Helt rigtigt at de vil fordele på 4 punkter i deres tabel over dim på bærlinger, ellers bliver deres tabel kæmpestor og passer ikke i lommeformat.
Ønsker du 2,4 meter mellem plinterne og opfylde kravene for c/c 600mm, må du gå op i limtræ eller en anden type bjælke da de kun har op til 220 høje K24 bærlinger i deres tabel.
se side 20 for limtræ bjælker, men du må grave dybere for samme højde.
vedrørende bonusspørgsmålet er det sådan, at man starter dim fra hvor man har lasten dvs. gulvet, så tjekker man tykkelsen mod c/c på gulvbjælkerne og derefter mod bærlingen og bærlingen mod plint underlaget og derefter plinterne mod jorden. har du længere c/c end 600 bør man øge til 28 eller 34.
Alt handler om nedbøjning som er acceptabel. du vil ikke have at gulvet skråner 1 cm mellem reglarne hvis man står midt imellem. det får man, hvis man har for langt imellem eller for lav konstruktion på gulvet, prøv med en bærde 22 mm, stå midt på den med underlag c/c 400, 600, 800 og 1000 og du vil få forskellig nedbøjning på midten. det samme gælder for bærlingen bare det at den tager op last fra flere gulvbjælker og større områder af gulvet.
håber jeg er tydelig det er ikke let uden at tegne nogle gange.
Ønsker du 2,4 meter mellem plinterne og opfylde kravene for c/c 600mm, må du gå op i limtræ eller en anden type bjælke da de kun har op til 220 høje K24 bærlinger i deres tabel.
se side 20 for limtræ bjælker, men du må grave dybere for samme højde.
vedrørende bonusspørgsmålet er det sådan, at man starter dim fra hvor man har lasten dvs. gulvet, så tjekker man tykkelsen mod c/c på gulvbjælkerne og derefter mod bærlingen og bærlingen mod plint underlaget og derefter plinterne mod jorden. har du længere c/c end 600 bør man øge til 28 eller 34.
Alt handler om nedbøjning som er acceptabel. du vil ikke have at gulvet skråner 1 cm mellem reglarne hvis man står midt imellem. det får man, hvis man har for langt imellem eller for lav konstruktion på gulvet, prøv med en bærde 22 mm, stå midt på den med underlag c/c 400, 600, 800 og 1000 og du vil få forskellig nedbøjning på midten. det samme gælder for bærlingen bare det at den tager op last fra flere gulvbjælker og større områder af gulvet.
håber jeg er tydelig det er ikke let uden at tegne nogle gange.
Jeg overvejede dette et par gange til. Det er muligt at få 3 punkter, hvis gulvstrøerne ligger præcis på punktfundamenterne. Og eftersom den eneste grund jeg kan komme på til at cc mellem gulvstrøerne skal mindske parallelt med afstanden mellem punktfundamenterne er for at undgå at lasten fordeles på for få punkter, så burde ligningen være i trin/intervaller snarere end lineært.
Eksempel: d=2m -> cc 50 cm. Det værste for bjælken og en given last er da, hvis gulvstrøerne ligger præcis på punktfundamentet, fordi vi så kun har tre punkter, som belaster bjælken. Hvis jeg nu mindsker d til 1,9....1,8....1,7...1,6... så ændres intet, bortset fra at momentet mod punktfundamenterne mindskes (bjælkens bæreevne øges), fordi der stadig ikke kan blive mindre end 3 gulvstrøer mellem to punktfundamenter. Ved d = 1,5 opstår imidlertid situationen, hvor der kan blive 2 punkter, og den lokale kraft mod bjælken øges (givet ugunstig placering af last).
Altså burde retningslinjen være at cc skal være mellem d/4 og d/3, og mine cc 600 på d=2,15 er med andre ord helt okay
Med forbehold for at jeg helt har misset pointen
Eksempel: d=2m -> cc 50 cm. Det værste for bjælken og en given last er da, hvis gulvstrøerne ligger præcis på punktfundamentet, fordi vi så kun har tre punkter, som belaster bjælken. Hvis jeg nu mindsker d til 1,9....1,8....1,7...1,6... så ændres intet, bortset fra at momentet mod punktfundamenterne mindskes (bjælkens bæreevne øges), fordi der stadig ikke kan blive mindre end 3 gulvstrøer mellem to punktfundamenter. Ved d = 1,5 opstår imidlertid situationen, hvor der kan blive 2 punkter, og den lokale kraft mod bjælken øges (givet ugunstig placering af last).
Altså burde retningslinjen være at cc skal være mellem d/4 og d/3, og mine cc 600 på d=2,15 er med andre ord helt okay
Med forbehold for at jeg helt har misset pointen
Nej, ligger en last rakt ovanför plinten bliver der intet moment i bærrebet for den overhovedet, dvs moment af 3 laster i stedet for 4 som du får ved understøttelse når plinten er midt mellem 2 gulvregler.
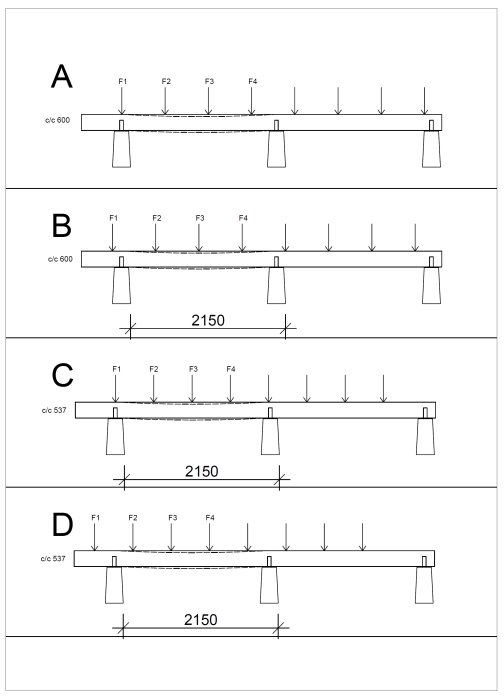
Moment er en bevægelse og når du stopper bevægelsen får du en nedbøjning. kraften fra gulvbjælkerne skaber moment i bærrebet. (se fig gik ikke at holde sig fra at tegne)
Så de har D/4 for at være sikker at du skal klare dig.
Kommentar til figur,
I A og B har jeg c/c 600 som du vil have, A er lige over plint og B er værste fald man kan få med last midt mellem plinter dvs længste afstand til understøttelse (bliver største momentet eksponentielt når man tager kraft gange afstand)
I C og D er c/c reduceret til D/4 537 mm, dette giver da en lavere last per F1 - F4 sammenlignet med A og B. da hver gulvbjælke skal i A og B optage 0,6x1,55x2kN og i C og D 0,537x1,55x2kN
A og B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C og D for F1 - F4 = 1,66 + ,5kN = 2,16 kN
Forskel 2,36-2,16 = 0,2kN eller ca. 10% mere i A og B.
Når du får værste beliggenhed på begge ender du midt mellem understøttelserne dvs 2,15/2 = 1,075 m gange dette med tidligere resultat og du får 2,53kNm for A og B samt 2,32 kNm for C og D.
Dvs C og D vil have mindre moment end A og B.
Til sidst kan jeg være enig om at de bruger et trubt tal for at kalkulere rigtig cc afstand, men at lægge med en kurve at læse af for at opdele forskellige d med 3,5 til 4,5 i en eksponentiel kurve havde bare været besværligt.
Moment er en bevægelse og når du stopper bevægelsen får du en nedbøjning. kraften fra gulvbjælkerne skaber moment i bærrebet. (se fig gik ikke at holde sig fra at tegne)
Så de har D/4 for at være sikker at du skal klare dig.
Kommentar til figur,
I A og B har jeg c/c 600 som du vil have, A er lige over plint og B er værste fald man kan få med last midt mellem plinter dvs længste afstand til understøttelse (bliver største momentet eksponentielt når man tager kraft gange afstand)
I C og D er c/c reduceret til D/4 537 mm, dette giver da en lavere last per F1 - F4 sammenlignet med A og B. da hver gulvbjælke skal i A og B optage 0,6x1,55x2kN og i C og D 0,537x1,55x2kN
A og B F1 - F4 = 1,86kN + ,5kN = 2,36 kN
C og D for F1 - F4 = 1,66 + ,5kN = 2,16 kN
Forskel 2,36-2,16 = 0,2kN eller ca. 10% mere i A og B.
Når du får værste beliggenhed på begge ender du midt mellem understøttelserne dvs 2,15/2 = 1,075 m gange dette med tidligere resultat og du får 2,53kNm for A og B samt 2,32 kNm for C og D.
Dvs C og D vil have mindre moment end A og B.
Til sidst kan jeg være enig om at de bruger et trubt tal for at kalkulere rigtig cc afstand, men at lægge med en kurve at læse af for at opdele forskellige d med 3,5 til 4,5 i en eksponentiel kurve havde bare været besværligt.
Klik her for at svare