How does one calculate buckling for a hollow post? Conditions: The post is composed of four standing wooden studs of arbitrary dimensions that are screw-glued along the entire joint. The studs are braced with noggings in both directions (y- and z-axes) at regular intervals to reduce the propensity for buckling.
Is it in the same way as a square bar compared to a square tube? Do you consider the joints to be as strong as the rest of the material?
...or do you take the values for a pole with the same outer dimensions as the hollow pole minus the values for a pole with the same outer dimensions as the hole on the inside?
Calculating joints is more advanced than what I can do, so either we have to assume that these have at least the same strength values as the other woodwork. Doing as you described in post 4 works excellently.
One problem with this procedure is that you constantly get buckling across the grain direction, which results in a much lower strength.
Why do you want to do it this way?
One problem with this procedure is that you constantly get buckling across the grain direction, which results in a much lower strength.
Why do you want to do it this way?
Do you have a picture of what you mean? I don't quite understand what you mean by reinforcing noggins. In general, you'll obviously get a much stronger column the larger the outer dimensions you can make on the column.
I don't know how to calculate or relate to joints on wood material. But it probably won't be terrible if you screw and glue.
I don't know how to calculate or relate to joints on wood material. But it probably won't be terrible if you screw and glue.
I'm not quite sure why the buckling direction would be different with a composite post than with a solid one. The pressure is in the direction of the grain in both cases. The reason I'm asking is that we have an existing hollow column and I want to calculate approximately what solid dimension this corresponds to since there is an old k-drawing where the solid dimension is specified (which someone apparently deviated from during construction). Below is a sketch showing the composition and also showing how the noggings are positioned (though it should probably say x and z instead to be completely correct, I blame the glögg).huggan said:
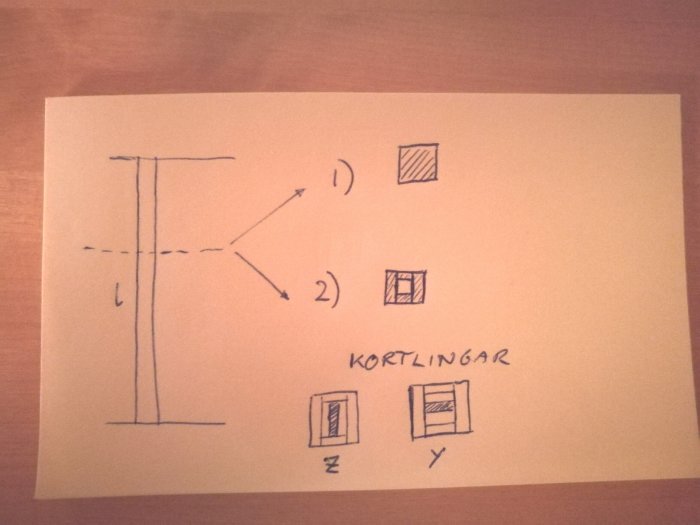
Last edited:
It is only in the longitudinal direction that there is load
Now I've dug up an old Hållf formula collection and the moment of inertia for thick-walled square tubes is indeed equivalent to the outer post minus the inner post. For thin-walled tubes, it was different, but that's not the case here.
Ok, thanks for the picture. It was as I thought. If you're worried about the load, you can reinforce it with additional posts on the outside of your pipe 
from a strength perspective, it won't get worse. Now I'm mainly thinking if your drawing states that it should be solid with side L and they made it hollow with side L. However, if it is hollow but slightly larger than side L, I wouldn't be particularly worried. It becomes stronger with side L squared, so it's enough to increase side L by the square root of 2, i.e., 41 percent, to get a post twice as strong (in that buckling direction).
Hope this makes things a bit clearer. Best wishes!
from a strength perspective, it won't get worse. Now I'm mainly thinking if your drawing states that it should be solid with side L and they made it hollow with side L. However, if it is hollow but slightly larger than side L, I wouldn't be particularly worried. It becomes stronger with side L squared, so it's enough to increase side L by the square root of 2, i.e., 41 percent, to get a post twice as strong (in that buckling direction).Hope this makes things a bit clearer. Best wishes!
I haven't had the chance to measure it properly yet, but if I find that it's too weak, would it be enough to apply thicker material without it resting on the plate and lying against the roof beam? The risk of deflection in the remaining centimeters should indeed be negligible. From a design standpoint, deflection should occur on the reinforced post long before maximum pressure happens on the unreinforced centimeters. Or am I thinking wrong here?
You can calculate it this way in this case too, but I would keep the usage rate very low to compensate for the fact that the joints are weaker than solid wood.Karl_Pedal said:
I am not such an experienced designer to confidently say how much extra safety margin you need, but I would guess a usage rate around 50% of the allowable load on a homogeneous tube-shaped cross-section.
Now I have checked and the existing pole is too weak. Then the follow-up question is: Which wood or panel material has the best properties for supplementation without adding too much?