Det svenska elsystemet del 1
Ofta sticker det upp en svart kabel ur källargolvet som strömmen kommer genom, vilket man kanske tar för givet, och att det är en garanti för ström. Ibland kommer strömmen via luften också... Men varifrån kommer kabeln? Hur ser det ut på utsidan huset?
Om man sedan tittar på kablar och luftledningar så finns där tre, fyra och ibland fem ledare. Hur hänger allt detta ihop rent tekniskt? Hur kan man göra tre ledare till fyra? Och den där skyddsjorden, vad är det och varför finns den, egentligen? Elvispen har ju ingen skyddsjord.
I kommande avsnitt kommer vi även att titta lite lätt på hur det ser ut på insidan av huset fram till elcentralen. Det blir även ett kapitel med en Husmors bruksanvisning för elcentralen och vi avslutar med ett om "Varför detta jorduttag?".
Sida 1 av 7
Elens väg till hemmet
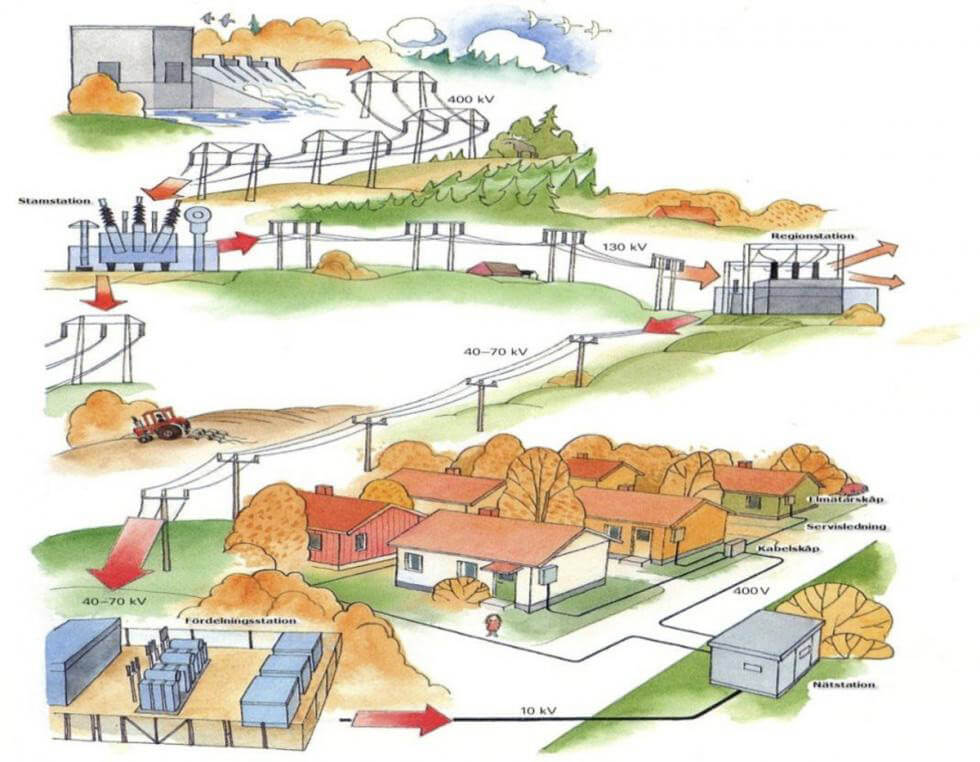
Elens väg till hemmet. Grafik: Elverket
Strömmen kan ha en lång väg att vandra fram till varje hus. Detta sveper vi snabbt förbi i ett kort stycke.
Från elkraftverken transporteras energin via stamnät, regionnät och lokalnät. De har olika spänningsnivåer och ägs av olika nätföretag. Stamnätet transporterar el från stora elproducenter till regionnäten. Regionnäten transporterar elen vidare till lokalnät och ibland till elanvändare med stor förbrukning, till exempel industrier. Lokalnäten distribuerar elen till hushåll, affärer, industrier med mera inom ett visst område.
Hela denna kedja behandlas inte här, utan endast den allra sista biten fram till huset, och lite om vad som finns inom huset. Vi kommer att gå igenom hur strömmen kommer in i huset den sista biten efter den närmaste transformatorn. Mycket kommer att handla om den magiska och mytomspunna ”nollan” vilket innebär att vi kommer att gå igenom begrepp som
• Trefassystemet, dess egenskaper och egenheter.
• Systemjordning, begreppen TN-C och TN-S.
• Skyddsjordning, som inte är detsamma som (system)jordning.
• Neutral- (N), skyddsjords- (PE) och PEN-ledare.
Sida 2 av 7
Trefassystemet
Förutom nollan så finns det faser. Att det behövs två trådar för att kunna skicka ström genom en lampa är inte så komplicerat att förstå. Det skulle där räcka med en fas (och en nolla). I Sverige distribueras emellertid tre faser som bilden ovan visar. Vad är nu bra med det? Jo, fördelen med detta är att det ger ett naturligt roterande magnetfält som passar motorer alldeles utmärkt. Det är annars svårt att få en motor att rotera åt ett bestämt håll.
De tre faserna är nämligen förskjutna i tid mellan varandra, det vill säga de har sin toppspänning efter
varandra i tiden.
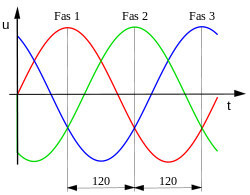
Se bilden ovan. Vid det ögonblick som Fas 1 (röd) har sin toppspänning så har både Fas 2 och Fas 3 samma negativa spänning som synes av bilden. (Spänningen mäts ”lodrätt” mellan kurvan och x-axeln, eller mellan kurvorna för två faser.)
Om vi vid detta ögonblick då Fas 1 har sin toppspänning skjuter tiden framåt lite så ser man att
spänningen i Fas 3 (blå) fortsätter att minska, medan den ökar i Fas 2 (går från negativ till positiv),
men minskar i Fas 1.
Det viktiga är att faserna har sitt toppvärde efter varandra vilket ger en ”riktning” som kan utnyttjas för att få motorer att snurra åt rätt håll.
Förutom de tre faserna finns även en neutral i våra hus, en nolla som är x-axeln i diagrammet ovan. Denna gör att vi pratar om två olika spänningar, 230 V och 400 V.
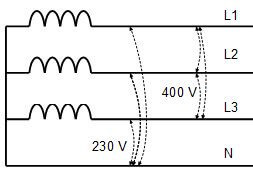
Bilden ovan visar ett vanligt sätt att avbilda detta system, med de tre faserna överst och nollan underst. Nollan är alltså en mittpunkt i systemet.
Spänningen mellan två faser (huvudspänning) är 400 V och mellan fas och neutralledare (fasspänning) 230 V.
Varför blir det inte dubbla spänningen mellan två faser, 460 V? Det handlar återigen om tiden.
Spänningen mellan fas och neutral har inte sitt toppvärde vid samma tidpunkt som när spänningen mellan två faser har sitt toppvärde.
Mer om det nedan.
Utbredning av trefassystemet
Trefassystemet används i de allra flesta länderna, men Sverige är ganska ensamma om att använda trefas inne i bostäderna utan det är förbehållet industrier och verkstäder. Européer tycker att Svenskarna är lite knäppa som drar in trefas i huset, det är ju farligt!
Européer kan istället dra in 63 A enfas i husen – det är verkligen knäppt!
Sida 3 av 7
Var kommer nollan ifrån?
Om vi backar lite och tar en titt på högspänningsnätet igen så ser man där tre ledare i höga stolpar. Detta är en vanlig syn den sista biten fram till transformatorkoisken som matar bostäderna, eller transformatorn i stolpen som på bilden här. Det är vanligen 10 kV i dessa ledningar.
Men hur kan det endast vara tre ledare där? Det måste ju handla om de tre faserna, så var kommer nollan ifrån??
Kommer den via marken? Nej.
Tar den en annan väg? Nej.
Är det magi? Ja, den trollas fram!
Nollan, den skapas i transformatorn i stolpen enligt bilden nedan. Högspänningsnätet förmedlar helt riktigt tre faser som kopplas till transformatorn i en D-koppling. En D-koppling har ingen mittpunkt, men en sådan har man skapat på sekundärsidan genom att använda en Y-kopplad lindning där.

Vi har redan sett exempel på en liknande bild ovan, fast då enbart sekundärsidan, så svaret på gåtan fanns redan.
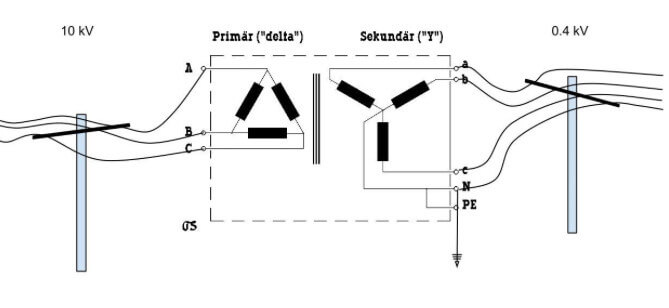
Magiskt! Transformatorn både transformerar ned spänningen och skapar en mittpunkt som vi kallar neutralpunkt. Om detta är den sista transformatorstationen, närmast abonnenten, så ligger högspänningen på 10-20 kV och lågspänningen på 230/400 V.
Sida 4 av 7
Jordtag
Det finns ett jordtag på bilden ovan som nollan är ansluten till. Det står även PE där vilket betyder att den har en skyddsfunktion. Det har ingenting att göra med nollan i sig och de två spänningarna 230 V och 400 V som skapas i transformatorn.
Jordtaget gör att man man ”ta” i nollan utan att få ström genom kroppen, men det har ingenting med dess funktion som nolla att göra.
Jordtagets funktion kommer vi in på senare under Systemjordning och skyddsjordning, och jordtagets egentliga syfte kommer eventuellt i en senare artikel.
Just nu nöjer vi oss med att neutralpunkten ser ut som den gör och vanligen distribueras som en kombinerad nolla och skyddsjord, en PEN. Så det som sticker iväg åt höger på bild är tre fasledare och en PEN-ledare.
Sida 5 av 7
Hur kan man trolla bort nollan?
Kan man trolla fram nollan så kan den trollas bort också.
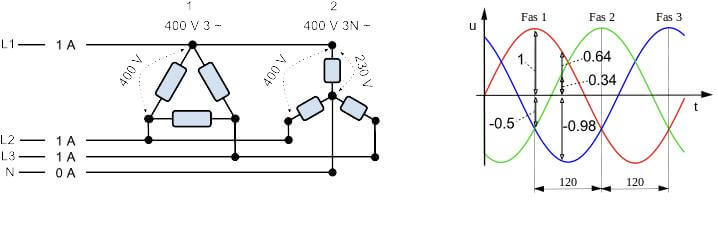
Det är allmänt känt att en trefasmaskin som belastar alla tre faser lika mycket inte behöver någon nolla. Om man ser på exemplet ovan så ser vi apparaten till höger utformad som ett Y (upp-och-ned-vänt) för att visa att den består av tre stycken interna förbrukare inkopplade mellan varsin fas och nollan.
Om dessa tre värmeelement eller vad det nu kan vara har samma effekt så kommer det i exemplet inte att flyta någon ström i neutralledaren. Man kan lika gärna koppla bort nollan, den behövs inte.
Varför blir det så då?
Det går att visa på olika sätt. Vi kan återvända till sinuskurvorna för de tre faserna och tänka oss att de visar strömmen i de tre faserna. Ta en linjal och mät avståndet mellan toppen av Fas 1 och nollan som är x-axeln. Mät sedan avståndet från nollan rakt ned dit Fas 2 och Fas 3 skär sina linjer. Hur är förhållandet mellan dessa två avstånd? Om avståndet mellan Fas 1 och nollan är 1 så är avståndet mellan nolla och Fas 2 och 3 lika med 0.5. Så om man då summerar dessa tre värden, då blir ju summan noll!
Givetvis kan man räkna på det också. Fas 1 har sin toppström vid 90 grader, medan Fas 2 ligger 120 grader efter Fas 1 och Fas3 ligger 240 grader efter.
î1 • sin(90) → 1.0
î2 • sin(90-120) → -0.5
î3 • sin(90-2*120) → -0.5
Ovanstående beräknades vid den tidpunkt få Fas 1 har sin högsta värde, vid 90 grader. Men oberoende av tidpunkt så kommer summan att bli noll. Det ser man genom att addera valfritt värde på de tre vinklarna, summan blir fortfarande noll.
î1 • sin(50+90) → 0.64
î2 • sin(50+90-120) → 0.34
î3 • sin(50+90-2*120) → -0.98
î1 • sin(651906+90) → 0.59
î2 • sin(651906+90-120) → -0.99
î3 • sin(651906+90-2*120) → 0.40
Förutom Y-koppling kan förbrukare kopplas in mellan faserna också, som ett D som exemplet till vänster ovan visar. Där är ju inte nollan med alls så givetvis kan det inte gå någon ström i nollan heller.
Om nu inte strömmen skulle vara lika hög i de tre faserna, då blir höjden på de tre sinuskurvorna olika, och man förstår då att summan inte blir noll längre, utan det kommer att flyta en ström i nollan. Denna ström kan man beräkna med sinussatsen eller med vektoraddition.
Sida 6 av 7
Förhållandet mellan fasspänning och huvudspänning
Om vi återvänder ett ögonblick till det två spänningarna, fasspänningen 230 V och huvudspänningen 400 V.
Det allmänt kända förhållandet dem emellan är √3, ca 1.73. Men i sinuskurvan ovan (om vi tänker oss att den visar spänningarna) ser det ju ut som om förhållandet skulle vara 1.5 om man tittar vid tidpunkten 90 grader då Fas 1 har sitt toppvärde. Ja, förhållandet är bevisligen 1.5 mellan Fas 1 – 2 (detsamma mellan Fas 1 – 3)! Så var kommer då √3 ifrån?
Jo, vid 90 grader så har inte spänningen mellan Fas 1 – 2 sitt toppvärde, utan toppvärdet kommer 30 grader senare. Det kan synas vara lika stort avstånd mellan Fas 1 och 3 där, men kurvan för Fas 1 är flack medan den för Fas 3 är brant.
I sinuskurvan har spänningarna ritats ut vid en punkt 50 grader senare, och man ser där att förhållandet är högre än 1.5, nämligen 0.64 + 0.98 = 1.62. Toppvärdet mellan Fas 1 – 3 har där precis vänt nedåt.
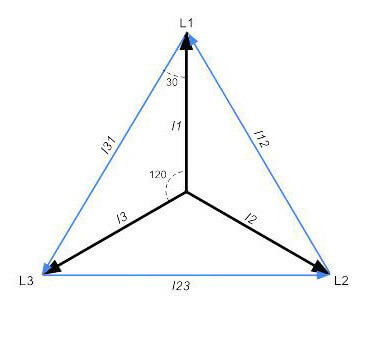
Om vi flyttar tillbaka tiden 20 grader till 120 grader så hittar vi toppspänningen mellan Fas 1 och 3 med förhållandet √3 mot fasspänningen. Detta ser man enklare med ett visardiagram som på bilden här.
Diagrammet roterar åt vänster (motsols). Just nu visar det Fas 1 vid 90 grader. Men om man vrider den 30 grader till motsols så ser man att huvudspänningen L1 – L3 får sitt toppvärde.
Med lite enkel trigonometri ser man också förhållandet mot fasspänningen som 2cos(30) = 1.73.
Sida 7 av 7
Det svenska elsystemet - alla delar
Den här artikeln är en del i artikelserien "Det svenska elsystemet" som består av fem delar:
del 1 - Det svenska elsystemet
del 2 - Det svenska elsystemet - systemjordning och skyddsjordning
del 3 - Det svenska elsystemet - inne i bostaden
del 4 - Husmors bruksanvisning för elcentralen
del 5 - Det svenska elsystemet - jordtag, jordning och jordfel

Kommentarer
167